深度学习：单元视角下多边形面积学习策略研究——以关键课《三角形的面积》为例

深度学习：单元视角下多边形面积学习策略研究——以关键课《三角形的面积》为例

朱佳静

浙江省桐乡市振西小学  314500

【摘要】小学阶段非常注重培养学生的数学思想。笔者以人教版五上“三角形的面积”一课为例，基于单元视角，通过奠定单元学习的“落脚点”；优化单元学习的“蓄力池”；搭建单元学习的“脚手架”；登上单元学习的“瞭望塔”四条螺旋上升的策略有效地解决单元视角下三角形的面积的学习，在教学过程中利用合作探究、教师点拨等方式时，十分关注学生转化思想和模型意识的建立，帮助学生养成良好的逻辑思维能力，助力单元视角下多边形面积的学习。

【关键词】深度学习；单元视角；转化思想；模型意识

一、打破固有思维，奠定单元学习的“落脚点”

“思维定势”是“教”和“学”中易进入的误区。单元视角下的面积教学，我们可以尝试打破常规，思考学习更优路径。

（一）起点重梳，关注学生认知原点

在教学前，对五年级8个班不同水平的学生（城区校区和农村校区）进行了前测，

了解到，大部分学生对平行四边形和三角形的面积公式是早有了解的，但是同学们对三角形面积公式中为什么要除以2是不清楚的，对公式更多的停留在记忆阶段。在引导学生利用转化求平行四边形面积时，同学们能够将平行四边形转化成熟知的图形，虽然同学们还未学习过三角形的面积计算，但是将平行四边形转化成长方形和转化成三角形的人数差不多。其实，从理论角度看，三角形是最基础的图形，平行四边形、梯形、圆等多边形的面积都可以转化成若干个三角形进行面积推导。可见，多边形面积的教学可以从《三角形的面积》入手，符合学生的认知起点。

（二）框架重构，实现进阶整体教学

在《多边形的面积》中，教材安排先学习平行四边形面积，继而学习三角形，梯形，组合图形的面积。在教学平行四边形面积时，受到长方形、正方形面积计算的影响，同学们很容易出现领边相乘。但面对基础的三角形，不易出现此情况。而且在平行四边形面积推导时，我们常常利用数格子或者剪拼法。受此基础影响，如果在学习三角形或梯形时，如果不提供多个相同的学具，学生是很难想到利用“倍拼法”求图形的面积。如果将《三角形的面积》作为起始课，链接教材“你知道吗？”中提到的“方田章”以及刘徽的“出入相补”原理，培养学生的探索精神和发散思维。

二、依托学习方法，优化单元学习的“蓄力池”

（一）合作探究，突破思维固化局限

在学习《三角形面积》时，课堂一开始就为学生提供合作探究的学习任务：

师：请同学们在长方形中画一个三角形，使得三角形的面积为长方形面积的一半？

在合作探究，小组讨论后，学生得到了以下几种方案；

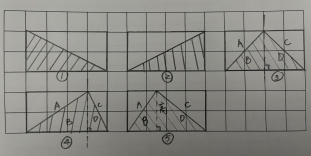
师：你们怎么证明这些三角形的面积是长方形面积的一半呢？

生：沿着长方形的对角线剪开，两个三角形能够重叠在一起，所以三角形的面积是长方形面积的一半。

生：沿着中间那条线把三角形剪开，剪开之后又变成两个长方形，再将长方形沿对角线剪开之后，A和B能重叠在一起，C和D也能重叠在一起。

师：中间那条线指的是什么？

生：是高。

生：图4的做法和图3的做法是一样的。

师：那图5呢？沿着哪里剪？

生：需要作一条高，沿着“高”剪。

师：同学们，你们真的太棒啦！

在组内探究和组间互助的过程中，学生的思路慢慢清晰。这个过程既提高了同学们合作探究的能力，又为接下来图形的转化提供灵感和借鉴思路。

（二）教师引领，拨开思维屏障迷雾

同学们对直角三角形的转化有探讨之后，想利用类比推理去推导锐角、钝角三角形的面积，但面对钝角三角形时遇到难题，它的“高”在三角形的外面，利用剪拼和倍拼法得到的长方形的长与宽和三角形的底和高关系不大，同学们陷入迷茫。

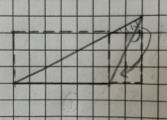
师：同学们，你是把那条边做“底”，那条边做“高”？

生：学生立马指出。

师：三角形有几条“底”，对应几条“高”

生：有三条。

生：老师，我想到了，如果我把钝角三角形进行旋转，把长边做“底”，那它和锐角三角形就一样啦！

教师引领，为学生模型构建推波助澜，拨开学生思维迷雾。

三、根植数学思想，搭建单元学习的“脚手架”

（一）多元转化，优化面积推导途径

在学习《三角形面积》时，呈现锐角三角形、直角三角形、钝角三角形。

师：同学们，下面三个三角形你最先想求哪个的面积？

生：直角三角形，它最方正。

师：请你把你的想法画下来？并说一说

生：我是通过数格子的。

师：这是一种好方法，谁还有更快的解决方法呢？

生：把直角三角形补成长方形，长方形的面积是长（三角形的底）×宽（三角形的高），所以三角形面积为底×高÷2

生：将三角形沿着一条直角边和一条斜边的中点剪开，然后拼成长方形，这时长方形的面积是长（三角形的底）×宽（三角形的高÷2），所以三角形的面积为底×（高÷2）。另一种长方形的面积是长（三角形的底÷2）×宽（三角形的高），所以三角形的面积为（底÷2）×高。

师：同学们，你们的思维真开阔，同学们，图4谁能解释一下？

生：这个做法师错误的，剪下来的三角形要小，补上去的三角形要大。

生：图5是一步一步移，最后和图

3是一样的。

在学习直角三角形的面积时，除了数格子以外，同学们不仅能想到“倍拼法”，还想到了“剪拼法”，为后续模型构建奠定基础。

（二）模型构建，实现特殊走向一般

在学习《三角形面积》时，在教师引领和学生合作探索之后，同学们从特殊到一般，完成三角形面积公式的推导。

师：同学们，你们有什么发现吗？

生：我们都是把三角形转化为长方形。

生：既可以剪拼法，又可以倍拼法。

生：都和三角形的“高”有关。

生：所以三角形的面积=底×高÷2

在活动探索中以层层递进的方式由特殊到一般总结三角形的面积公式。给与学生充分的感知、操作机会，对三角形的面积公式由刚开始的死记硬背到最后刻画于心。

学习数学，最重要的不是数学知识的教学，而是学生主动习得数学思维、数学思想方法的教学。基于单元视角，在教师引导下，主要在学生自主提问，认知冲突，充分合作中解决问题，帮助学生提升数学核心素养。