南京邮电大学 210046
摘要:随着科技的发展,M序列密码作为周期达到最大值的序列密码,更加广泛地应用于通信系统、密码学和序列分析等领域。在项目中,我们将通过系统的逻辑信息、结点之间的连接信息的分析将布尔网络的局部收敛性和快速稳定性作为判断依据,以使得计算复杂度得到降低。并且,我们对这一项目在人工智能上的应用进行论述,为基于布尔网络构造的M序列密码的实际应用提供更多可能性
一、项目背景
近些年,基于布尔网络方法研究序列密码引起广泛关注。
在矩阵半张量积工具的帮助下,序列密码生成器(包括线性反馈移位寄存器、滤波器等)能够被唯一表示为离散的线性系统,在此基础上关于布尔网络的许多分析方法被应用到序列密码的分析和构造中,取得了一系列丰富的研究成果。相较于传统的基于代数方法的多项式表示法,利用布尔网络方法能够通过状态转移矩阵来体现所有状态转移的信息,更便于对流密码的分析和构造,且从转移矩阵中能够直接得到其对应的逻辑表达形式,这有助于其电路设计的实现。
二、研究目的
利用布尔网络方法研究M序列的构造问题,实现计算复杂度的降低并且将相关结果应用到日常生活中。
通过大量的文献检索,我们发现M序列密码的构造方法还有待进一步研究,现有文献大多基于代数方法来研究M序列的构造问题,但所提出的方案计算复杂度过高并且应用场景还有待进一步扩展。
三、项目研究内容
我们将利用离散微分、拓扑结构分析法设计实验方案,采集部分加密数据,并且针对这些算法设计实验方案。
微分数值计算是一种解决微分方程的数值方法。它把不可解的非线性微分方程拆分成可解的离散问题,并以相当简单的方法求出最优解。这种方法求解的结果又称为微分数值解。它通过反复准确地计算函数值,并用微分方程来确定函数在某一时刻的导数和瞬变量,从而求得连续的函数解。
采集到加密数据后,对其进行离散微分分析,可将原始数据序列转化成一组离散的差分序列,获取更多的数据信息,如数据的变化趋势和周期性。之后,用到图论的知识进行拓扑结构分析,将系统建模为拓扑结构。
利用拓扑结构分析法对密码学中常用的一类加密算法进行了分析,并根据其数学模型给出了实现该算法的拓扑结构,便于设计出更好的加密算法,并且在保证一定安全性能的情况下,减少加密数据量。
利用离散微分法来计算每条数据的微分方程,然后利用拓扑结构分析法来对每条数据进行还原,最后通过对比两种方法得到的结果,判断出加密后的数据。
四、项目创新点
1、灵活性高
布尔网络有0和1两个状态,下一个节点的状态是由相邻节点决定的,它可以通过不同门电路组合实现不同的控制逻辑,从而构造出不同的伪随机序列。
2、抗干扰能力强
由于布尔网络模型是一种以有向图为基础的离散系统,它的结构相对分散,相比于线性结构和树形结构等,每个节点受其它节点的影响相对较小,可以抵抗一定的外来的干扰。
3、具有很强的延展性
布尔网络的离散结构让它可以很容易实现网络延展,使M序列周期更长,其随机性更高,密码的安全性也更高。
4、功耗较低
布尔网络有0和1两个状态,下一个节点的状态是由相邻节点决定的,它可以通过不同门电路组合实现不同的控制逻辑,从而构造出不同的伪随机序列。
五、项目研究过程
1、基于布尔网络方法构造M序列密码
借助矩阵半张量积、结合布尔Perron-Frobenius定理,将状态转移图转化成矩阵形式,通过运算得到状态转移矩阵和其布尔表达式。
2、构造M序列密码算法的优化
尝试利用布尔网络方法对反馈移位寄存器进行改造,通过布尔网络构造下的M序列的特性研究,使计算复杂性得到降低。
3、对优化后的布尔网络构造M序列密码进行分析
利用离散微分、拓扑结构分析法采集部分加密数据并分析,优化实验方案。
4、完成布尔网络构造M序列密码的实际应用
实现了使用M序列密码对图像进行加密,用以展示序列密码实际应用,给出具体算法代码,为基于布尔网络构造的M序列密码的实际应用提供更多可能性。
六、研究成果与成效
经过为期一年的研究与实践,我们团队基于布尔网络的方法在研究反馈移位寄存器的构造问题上取得了一些成果。
1、Galois型反馈移位寄存器和Fibonacci型反馈移位寄存器的转换




2、构造一个全局稳定且单调的反馈移位寄存器


3、模拟传统的反馈移位寄存器及Galois反馈寄存器
在MATLAB环境中,我们利用这些理论成果,成功模拟生成了具有特定性质的M序列。

图1 模拟传统的反馈移位寄存器生成M序列密码

图2 模拟Galois反馈寄存器生成M序列密码
这些M序列在通信、密码学等领域具有广泛应用,其全局稳定性和单调性保证了数据传输的可靠性和安全性。
3、线性反馈移位寄存器与二叉决策图(BBD)在布尔网络中的优化策略
首先我们重温一下什么是布尔函数:
布尔函数(Boolean function):描述如何基于对布尔输入的某种逻辑计算确定布尔值输出,它们在复杂性理论的问题和数字计算机的芯片设计中扮演基础角色。比如布尔函数 (
![]() ⊕
⊕![]() )⊕(
)⊕(![]() ⊕
⊕![]() )用下面的逻辑电路表示:
)用下面的逻辑电路表示:
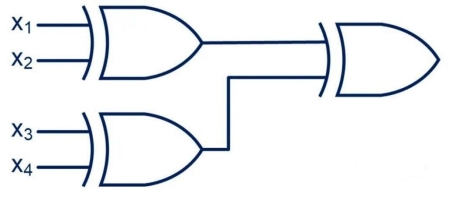
图3 布尔函数 (![]() ⊕
⊕![]() )⊕(
)⊕(![]() ⊕
⊕![]() )的逻辑电路图
)的逻辑电路图
为了解决大规模逻辑网络的处理带来的存储和计算资源的巨大消耗这一难题,高级数据结构如BDD(二叉判定图)以及分布式处理应运而生。BDD能够以紧凑且规范的方式表示布尔函数,通过共享子图减少冗余,从而显著减少所需的空间和时间复杂度;而分布式处理将逻辑网络分块处理,并在不同的处理器或计算单元上同时处理,可以有效地提高处理速度和效率。
1、算法一:二元决策树(BDD)
1>二元决策树的定义
二元决策树与二叉树在结构上类似,上面的逻辑电路(图3)/函数对应的有序二元决策树如下图:
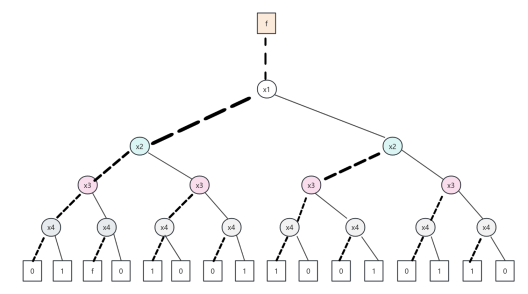
图4 逻辑电路(图3)函数对应有序二元决策树
BDD是实现布尔函数复杂逻辑设计和验证的强有力工具,他通过共享子图、减少冗余来实现的以其紧凑和规范的方式表示布尔函数,减少了存储空间和计算需求。
它由一组节点和边组成,每个节点代表一个布尔变量,边代表逻辑运算(如AND、OR、NOT)。BDD通过限制每个节点的子节点数量,使得逻辑运算和解决方案的寻找更加高效。
2>二元决策树的构建
BDD的构建过程主要包括以下步骤:
(1)初始决策树:首先,根据布尔函数的逻辑结构构建二元决策树(BDT)。决策树的每个节点对应一个变量,根据变量的值决定沿着哪条路径继续。
(2)归约过程:然后,对决策树进行归约操作,以消除冗余和简化结构。归约过程包括合并具有相同子节点的节点(规则1),以及删除high边和low边指向相同子节点的节点(规则2)。重复应用这些规则,直到无法进一步归约为止。
(3)确保有序性:在构建BDD时,必须保证变量的出现顺序是一致的(即有序的OBDD),这样可以确保BDD的唯一性,便于后续的操作和比较。
(4)结果BDD:最终得到的归约有序的二元决策图(ROBDD或简称BDD)是一个紧凑的图形表示,能够高效地表示和计算布尔函数。
2、算法二:分布式处理
1>分布式处理的原理
分布式处理的基本原理是将大规模的逻辑网络分解成多个小规模的子网络,并在不同的处理器或计算单元上同时处理。这种方法可以通过并行处理和优化搜索策略,加快处理速度,提高处理效率。具体来说,可以将逻辑网络划分为不同的模块或节点,并在不同的处理器或计算单元上对每个模块或节点进行独立处理。
2>分布式处理的算法伪代码
算法:在分布式环境中处理布尔网络 |
输入:布尔网络 G(V, E),其中 V 是顶点集合,E 是边集合 |
输出:分块后的布尔网络列表 L,每个网络 G_i(V_i, E_i) |
函数 pideNetwork(G): |
创建空列表 L |
计算网络 G 的最大连通分量 C |
for each 连通分量 C_i in C: |
创建一个新的布尔网络 G_i(V_i, E_i) |
V_i = C_i |
从 G 中提取与 C_i 相关的边,更新 E_i |
将 G_i 添加到列表 L 中 |
返回 L |
函数 analyzeSubnetworks(L): |
for each 布尔网络 G_i in L: |
对 G_i 应用布尔网络分析算法,例如可达性分析、稳定性分析等 |
根据分析结果输出相关信息或采取行动 |
主程序: |
G = 构建布尔网络实例() |
L = pideNetwork(G) |
analyzeSubnetworks(L) |
3>分布式计算的优势与策略
分治策略:将大问题分解成若干小问题,每个小问题分配给不同的处理器或计算单元独立处理,最后再将结果整合起来。
动态规划:通过利用子问题的解来构造原问题的解,避免重复计算,提高处理效率。
优化搜索策略:根据具体问题和任务类型选择和调整策略,如启发式搜索、遗传算法等,以实现最佳处理效果。
通信和协调机制:采用专门的通信协议和协调机制,确保处理器或计算单元之间的有效协作和数据交换。
七、项目推广与应用
在密码学领域,我们利用所构造的反馈移位寄存器生成的M序列,提供了一种高安全性、高效率的序列密码生成方法。这种密码生成方法不仅保证了密码的随机性和复杂性,还通过全局稳定性和单调性确保了密码的可靠性和安全性。
在图像处理领域,我们利用生成的M序列密码对图像进行加密,有效保护了图像的机密性和完整性。这种加密方法具有简单易行、加解密速度快、安全性高等优点,可广泛应用于军事、金融、医疗等领域的图像保密传输。
参考文献
[1]熊飞,乔迪,王宏祥等.一种基于有序二元决策图和布尔函数性质计算网络可靠性的算法[J].电子与信息学报,2014,36(11):2786-2790.
[2]jacob闲人散鹤.二元决策图(Binary Decision Diagrams - BDD) (一)[EB/OL].(2021-08-06).https://zhuanlan.zhihu.com/p/397164596
[3]沈启峰,黄士坦,杨靓.AES中有限域运算的优化及算法高速实现[J].微机发展, 2005, 15(12):4.DOI:10.3969/j.issn.1673-629X.2005.12.006.
[4]李博文. 基于布尔网络的伪随机序列生成器分析与综合[D].东南大学,2022.DOI:10.27014/d.cnki.gdnau.2021.000065.
[5]易海博. 有限域运算和多变量公钥密码硬件的优化和设计[D].华南理工大学,2015.
[6]杨晓岚.基于云计算技术的分布式网络海量数据处理系统构建[J].无线互联科技,2023,20(2):68-70
[7]冯俊娥,李怡靓,赵荣.基于矩阵半张量积的有限值动态系统的最新进展[J].控制与决策,2022,37(02):267-277.DOI:10.13195/j.kzyjc.2021.1596.
[8]R. E. Bryant. Graph-based algorithms for boolean function manipulation. IEEE Transactions on Computers, C-35(8):677–691, August 1986.