基于SARIMA模型在我国公路货运量的预测研究

基于SARIMA模型在我国公路货运量的预测研究

刘绮霞

华南师范大学

摘要：本研究以中国统计年鉴2010年1月至2023年11月的公路货运量时间序列数据为基础。首先，对序列进行缺失值处理，采用线性插值方法填充缺失数据，以确保时间序列的完整性。接着，通过特征分析揭示了公路货运量数据的非平稳性、线性趋势和季节性特征。

在平稳性处理阶段，采用了差分方法，旨在消除序列的线性趋势，并进一步提取序列的季节性成分将这一非平稳序列转化为平稳的序列，为接下来建立时间序列模型奠定基础。模型的选择过程中，通过对自相关函数图的观察，提出六个备选模型，通过AIC和SC的比较，结合参数检验结果，最终确定了作为最优模型。

关键词：线性插值，非平稳，SARIMA模型

1.引言

本文以2010年1月-2023年11月我国公路月度货运量时间序列数据为研究对象，针对铁路货运量时间序列数据具有长期递增趋势、季节性变动和不规则变动特征建立SARIMA模型，并预测未来公路货运量的发展趋势。

2.公路货运量分析及预测

2.1数据特征分析

对2010年1月至2023年11月我国铁路货运量数据初步画出时序图，其变化趋势如图1所示。由图1可知，公路货运量时间序列具有线性递增趋势，且呈现出明显的有规律的季节性变化，平均变动周期大致为12个月。

图1 我国铁路货运量数据序列的时序图

2.2数据平稳性检验

表1 公路货运量序列的ADF检验结果

由上表，P值为0.2023>0.05，说明不能拒绝原假设，说明序列存在单位根，即序列非平稳。做该时间序列的样本自相关函数图，见图2。

图2 公路货运量序列的自相关系数和偏自相关系数图

从图2发现，自相关函数呈线性衰减，且衰减速度缓慢，该序列含有一定的趋势性，并且从两者中都能发现该序列还具有周期长度大约为12的季节效应。

2.3数据平稳化处理

2.3.1消除趋势性

为了消除趋势性成分，对序列进行一阶差分处理，即

生产新的序列，做出其时序图，见图3。

图3 的时序图

通过上图，差分后序列的均值是稳定在零点附近的，即通过一阶差分后，原序列的去趋势性已经基本消除。

2.3.2消除季节性

对序列进行12步差分，得到新序列记为并画出其时序图，见图4。

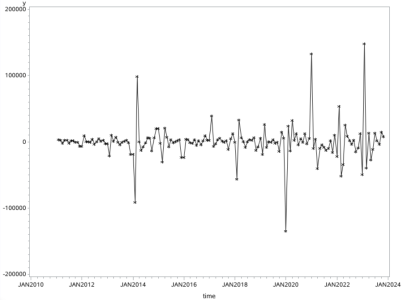
图4 的时序图

P<0.00001，拒绝原假设，说明序列不存在单位根，即季节差分序列已经平稳。

表2 序列的ADF检验

3.总结

本文基于时间序列分析方法，对我国公路货运量2010年1月至2023年11月的月度数据进行了建模与预测。首先，通过对数据的差分和季节性调整，得到了平稳的时间序列。接着，通过观察自相关和偏自相关图，初步选择了模型作为初始模型。

本研究建立的模型对中国公路货运量的预测具有较高的准确性和可解释性，为相关决策提供了参考依据。需要注意模型的预测受到外部因素的影响，实际预测结果可能因外部环境变化而发生调整。但是SARIMA模型本身也有先天性的缺陷，预测期的扩展,预测误差会逐渐增加。但在短期预测预测误差率较小，未来研究可以考虑引入更多外部因素以提高模型的预测精度。

参考文献

[1]李国辉,朱建良.利用无偏最优维数灰色预测模型预测我国公路货运量的发展[J].黑龙江交通科技,2005(01):90-92.

[2]樊志梅,赵联文,王永平.我国公路货运量的建模与预测[J].时代金融,2014(03):320-321.

[3]赵建有,周孙锋,崔晓娟等.基于模糊线性回归模型的公路货运量预测方法[J].交通运输工程学报,2012,12(03):80-85.

[4]张丽莉.基于神经网络的公路货运量预测方法研究[J].华中师范大学学报(自然科学版),2015,49(02):186-189.

[5]周志娟,陈森发.组合预测方法在我国公路货运量预测中的应用[J].中国水运(下半月),2010,10(05):166-167.