基于控制量参数化的A320客机下降段轨迹优化
秦鹏
(北京飞机维修工程有限公司西南航线中心天府航线大队) 四川 成都 610200)
秦鹏,男,高级工程师,大专,河北定兴,主研领域:空客飞机运行保障和技术状态管理。
摘 要针对A320客机下降段轨迹优化问题,采用控制量参数化的方法将问题转化为非线性规划问题进行求解,并利用约束转录法,增加优化可行域范围。实验仿真结果验证,在综合考虑下降时间与燃油成本的优化目标时,优化得到的客机下降段轨迹在满足A320客机性能约束以及乘客乘机体验的前提下能够达到下降高度以及速度,实现了A320客机下降段的轨迹制导设计。
关键词A320 轨迹优化 控制量参数化
关键词中图分类号 TP3 文献标志码 A DOI:
THE TRAJECTORY OPTIMIZATION OF A320 AIRCRAFT descending section BASED ON Control parameterization
Qin Peng
(Beijing aircraft maintenance engineering co. Chengdu 610200, Sichuan, China)
AbstractAiming at the trajectory optimization problem of the descending section of the A320 passenger plane, the control parameter method is used to transform the problem into a nonlinear programming problem for solving, and the constraint transcription method is used to increase the scope of the optimization feasible region. Experimental simulation results verify that when the optimization goals of descent time and fuel cost are considered comprehensively, the optimized trajectory of the descent section of the passenger aircraft can reach the descent height and speed under the premise of meeting the performance constraints of the A320 passenger aircraft and the passenger experience, realizing the descent of the A320 passenger aircraft Segment trajectory guidance design.
KeywordsA320 Trajectory optimization Control parameterization
秦鹏:基于控制量参数化的A320客机下降段轨迹优化
引 言
随着中国国民经济的增长与飞机自主研发能力的提高,中国民航业发展迅猛,客机数量日渐增多,人们飞机出行的占比越来越大。作为民用飞机管理系统的重要一环,飞机轨迹规划格外重要,影响着整体的机场调度管理与航空公司的收益。飞机整体的飞行阶段大致由起飞爬升、巡航与下降着陆三个部分组成。飞机飞行轨迹的规划必须考虑到飞行时间、燃油消耗量等与机场管理和经济消耗息息相关的因素[1]。
![]()

近年来,飞机轨迹优化问题已有颇多研究,如基于全局优化算法的一类研究:考虑到飞机最快时间爬升与最小燃油消耗,文献[1]采用遗传算法优化了飞机爬升轨迹,满足了飞机的物理性能限制,且考虑到乘客乘坐体验;文献[2]考虑飞机纵向飞行轨迹优化问题,采用改进微粒子群算法得到了Boeing737-800飞机的纵向飞行最优轨迹;文献3]考虑客机飞行阶段中的使用成本、总温室气体排放量以及两者组合的多目标性能,利用序列二次规划算法优化飞行轨迹
由于计算机性能的提高,通常使用数值法来解决此类问题,数值法主要分为直接法与间接法。其中直接法相比于间接法应用更加广泛[11]。直接法的思想为通过直接离散近似化状态量或者控制量来将原始问题转化为可求解的非线性规划问题,作为直接法中的一个重要分支,控制量参数化控制方法应用颇多。如文献[5]将控制参数化应用到工业典型控制中,并通过仿真实验得到了比较好的控制效果;在化工行业,文献[6]利用参数化方法求解了化工产业中的发酵过程控制优化问题,降低发酵过程成本和能耗成本;文献[7]则解决了以降低牵引能耗为目标的单车节能操纵优化问题。控制量参数化方法在实际工业生产中实际性较强,因此,综合考虑飞机飞行时间与燃油消耗,本文应用参数化控制方法来优化A320客机下降段飞行轨迹。并应用约束转录法来增加飞机飞行状态约束的可行性,提高轨迹优化迭代速度。
1A320客机下降问题描述
1.1客机垂直面运动方程
对于飞机巡航段之后的下降段飞行过程,考虑小攻角范围,忽略飞机发动机安装角,可采用飞机无侧滑、无倾斜的纵向飞行制导动力学方程[1]:
 (1)
(1)
式中,![]() 为飞机飞行速度,
为飞机飞行速度,![]() 分别为飞机的发动机推力和攻角,
分别为飞机的发动机推力和攻角,![]() 表示飞机侧向飞行距离与飞行高度,
表示飞机侧向飞行距离与飞行高度,![]() 为航迹倾斜角,
为航迹倾斜角,![]() 为A320的质量,对于民航客机,飞机质量随着燃料消耗量的增加而逐渐减小。
为A320的质量,对于民航客机,飞机质量随着燃料消耗量的增加而逐渐减小。![]() 为客机单位推力下每小时燃油消耗率。
为客机单位推力下每小时燃油消耗率。![]() 分别为A320飞机的升力与气动阻力,由下式得到
分别为A320飞机的升力与气动阻力,由下式得到
![]() (2)
(2)
![]() (3)
(3)
![]() 为空气密度,
为空气密度,![]() 为飞机机翼面积,
为飞机机翼面积,![]() 为阻力系数,
为阻力系数,![]() 为阻力系数,由飞行动力学可知,气动系数的主要影响因素为攻角
为阻力系数,由飞行动力学可知,气动系数的主要影响因素为攻角![]() 与马赫数
与马赫数![]() 。本文根据A320公开的气动数据,通过多项式插值拟合,可以得到升力系数与阻力系数可以进一步表示为[21]
。本文根据A320公开的气动数据,通过多项式插值拟合,可以得到升力系数与阻力系数可以进一步表示为[21]
![]() (4)
(4)
![]() (5)
(5)
拟合之后的各系数为:
 (6)
(6)
| (7) |
拟合效果如图1及图2所示。可以看到在小攻角范围及A320全马赫范围内,能够通过数值拟合建立较为准确的气动系数与攻角及马赫数的关系。
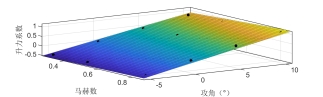
图1 A320升力气动系数拟合
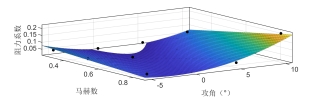
图2 A320阻力气动系数拟合
对于上述的A320下降段制导动力学模型,控制目标为:通过飞机攻角与发动机推力的直接控制,从飞机的巡航状态开始进入下降段,使飞机下降到合适的高度与速度为之后的着陆段做准备。其中在整体下降过程上,我们考虑最快时间下降与燃油最省的多目标优化,优化得到的飞机姿态与速度指令可作为制导指令,输入至后续相关的内环控制器,使飞机整体完成下降任务。
对于式(1)的客机垂直面运动方程,飞机运动方程的状态变量可以表示为
![]() (8)
(8)
控制输入为
 (9)
(9)
因此,客机爬升运动方程可表示为
![]() (10)
(10)
![]() (11)
(11)
![]() 为巡航段结束时的飞机状态,及下降段初始状态。
为巡航段结束时的飞机状态,及下降段初始状态。
1.2客机下降段轨迹优化问题
对于客机下降段轨迹优化问题,目标函数选为最快下降与最低燃油消耗的综合考虑。
(1) 优化目标函数。假设飞机爬升终端时间![]() ,同时考虑到飞机下降段的飞行时间与燃油消耗,将终端时间视为待优化的参数,通过最小化以下目标函数来选优化飞机下降段的轨迹
,同时考虑到飞机下降段的飞行时间与燃油消耗,将终端时间视为待优化的参数,通过最小化以下目标函数来选优化飞机下降段的轨迹
| (12) |
(2) 飞机下降段状态约束。考虑到飞机的物理限制与乘客体验,飞机下降时航迹倾斜角与飞机飞行马赫数![]() 应满足
应满足
![]() (13)
(13)
且对于一般民航要求,飞机起飞离地瞬间速度![]() 应该满足
应该满足![]() 。
。
考虑到飞机发动机推力限制以及乘客飞行体验,飞机发动机推力与过载系数不应过大,
![]() (14)
(14)
飞机开始下降时,应以巡航状态以及巡航高度开始,下降结束时应达到指定的下降速度与下降高度,即
 (15)
(15)
(13)式及(15)式的状态不等式及等式终端约束可以表示为下面更紧凑的形式:
| (16) |
本文考虑的客机下降段轨迹优化问题可以表示为如下典型的带有连续时间状态不等式以及等式约束的Boltza优化问题形式,即:
| (17) |
2参数化控制方法
2.1时间变换
在客机下降段轨迹规划问题中,终端飞行时间为待优化的参数,但在优化问题中终时不固定问题较难处理。这里我们应用时间变换的思想,将飞行时域由![]() 通过以下公式转换成虚拟域
通过以下公式转换成虚拟域![]() ,
,
![]() (18)
(18)
其中,![]() 为待优化的系统参数。经过上式的时间变换,(13)式可变为:
为待优化的系统参数。经过上式的时间变换,(13)式可变为:
| (19) |
2.2控制量参数化时间变换
参数化控制方法的思想是将连续时域内的控制轨迹用有限个多项式基函数进行近似,如将控制轨迹近似为若干段常值函数,这样,无限维的轨迹控制问题就转化为有限参数的优化问题。其大致步骤为
1)由2.1节的时间变换,控制优化问题转换为带优化参数的固定时间优化,优化区间为![]() 其,首先将区间分为有限个子区间,这里我们选择等分划分
其,首先将区间分为有限个子区间,这里我们选择等分划分![]() 个区间:
个区间:
![]()
那么第![]() 维控制量
维控制量![]() ,就可以由下列基函数近似表示
,就可以由下列基函数近似表示
![]() (20)
(20)
其中![]() 为待优化的分段控制参数,
为待优化的分段控制参数,![]() 为基函数,
为基函数,![]() 为开关函数,其具体表达式为
为开关函数,其具体表达式为
![]() (21)
(21)
这里我们选择将控制量分段常值化,即![]() 。这样控制量就由有限个常值参数来近似代替,如图3。
。这样控制量就由有限个常值参数来近似代替,如图3。
![]()



![]()
![]()
![]()
![]()
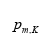
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
图3 控制量参数化近似
通过控制量参数化,客机下降段优化问题中的推力与攻角控制量可由下列参数化向量得到:

这样,无穷维的连续时间最优控制问题就转化成了有限维的非线性规划问题。
2)约束转化。虽然将A320下降段优化问题转化为了有限维的非线性规划问题,但其中的不等式约束如果不经过处理,很容易在优化迭代开始时就陷入无可行解的情况,因此我们采用约束转录法,将约束进行适当的放缩,增加迭代初始的可行域范围,提高收敛速度。对于不等式约束![]() ,其对状态量的约束等价于:
,其对状态量的约束等价于:
| (22) |
其中,

![]() 为约束精度,
为约束精度,![]() 为松弛变量。显而易见,当二者趋近零时,式(23)等价于原状态约束。且可以证明上述的状态变换方法不仅能够增加优化解初始的可行域并且满足最优解收敛定理[9]。经过以上处理,A320下降段优化问题可近似为以下非线性规划问题:
为松弛变量。显而易见,当二者趋近零时,式(23)等价于原状态约束。且可以证明上述的状态变换方法不仅能够增加优化解初始的可行域并且满足最优解收敛定理[9]。经过以上处理,A320下降段优化问题可近似为以下非线性规划问题:
| (23) |
将此问题称为问题1。下列给出了通过求解问题1得到A320下降段轨迹优化原始问题的最优解的算法流程。
Step 1:初始化![]() ;
;
Step 2:求解问题1,并将最优解![]() 带入A320运动方程(1),通过更新的状态量,检查原始不等式约束
带入A320运动方程(1),通过更新的状态量,检查原始不等式约束![]() 是否满足,若满足则跳转至Step 4,若不满足,跳转至Step 3;
是否满足,若满足则跳转至Step 4,若不满足,跳转至Step 3;
Step 3: 令![]() ,跳转至Step 2继续求解;
,跳转至Step 2继续求解;
Step 4: 令![]() ,若
,若![]() 则跳转至Step 2继续求解,否则停止算法;
则跳转至Step 2继续求解,否则停止算法;
3仿真实验及分析
3.1实验参数设置
本文研究空客A320客机的下降段轨迹优化问题,客机巡航马赫数![]() ,巡航高度为8000m,下降结束时目标马赫数为0.5,高度为100m。过载系数过大会导致客机飞行状态变化过大,考虑乘客乘机体验,飞机过载系数不超过1.2。A320飞机基本机型参数设置与推力、攻角和倾斜角范围设置如表格1。控制量参数化总区间个数
,巡航高度为8000m,下降结束时目标马赫数为0.5,高度为100m。过载系数过大会导致客机飞行状态变化过大,考虑乘客乘机体验,飞机过载系数不超过1.2。A320飞机基本机型参数设置与推力、攻角和倾斜角范围设置如表格1。控制量参数化总区间个数![]() 。
。
表1飞机参数设置
参数 | 取值 |
机翼参考面积(m2) | 122 |
巡航结束重量(kg) | 53782 |
飞机最大推力(KN) | 145.2 |
航迹倾斜角(deg) | [-25,25], |
马赫数 | [0,0.82] |
过载系数 | [0.8,1.2] |
3.2实验结果分析
图4为应用本文算法所得到的A320下降段最优轨迹。图5为A320高度变化。分析可得,A320客机客机巡航段结束后,先以比较大的坡度下降,这是由于优化时考虑到了下降时间,到一定高度后下降比较平缓,而后下降到指定高度后,推力持续减小,这是由于优化时同时考虑了燃油成本,减速至目标马赫数后下降段结束。总的下降时间为225.7s,燃油消耗为169.4kg。
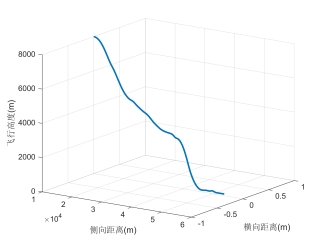
![]()
图6及图7分别为A320的马赫数与倾斜角变化,可以看到A320在下降较快的0-50s左右,速度整体为
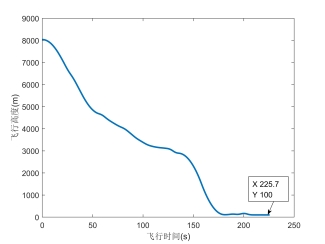
图5A320高度变化
增加的趋势,这是由于A320重力势能转化为了动力势能。而且在50s-140s左右的下降时间段,为了节约燃油消耗,尽量用小推力飞行,进而飞行速度降低;最后一段下降过程中,速度增加,达到指定高度后,平飞一段时间使飞机减速至目标马赫数。在此过程中,A320倾斜角始终在要求的范围内。
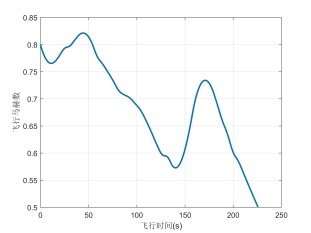
图6A320马赫数变化
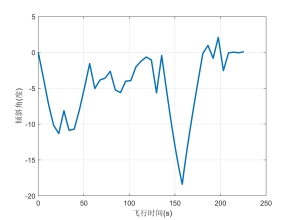
图7 A320航迹倾斜角变化
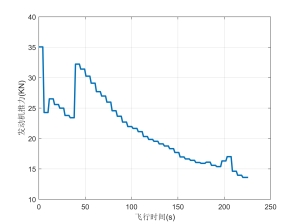
图8 A320推力变化
图8为发动机推力变化。可以看到为了缩短下降时间与降低燃油成本,飞机下降时主要考虑重力势能的转化,发动机推力较小,能够在快速下降的同时降低燃油消耗。
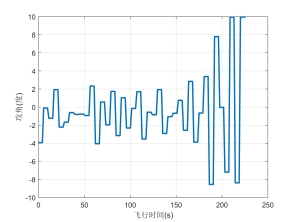
图9 A320攻角变化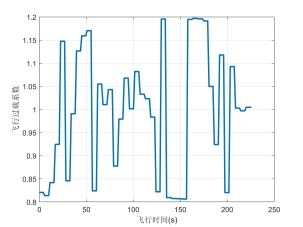
图10 A320过载系数变化
图9和图10分别为攻角与过载系数变化可以看到飞机攻角始终在设置的小范围内,且过载系数也在乘客舒适范围内。综上,对于A320客机下降段轨迹优化问题,综合考虑飞行时间和燃油消耗,本文提出的方法化所得的下降轨迹满足客机下降段要求,并且在考虑乘客乘坐体验的同时,飞行状态满足A320物理性能要求。
4结 语
本文应用控制量参数化方法对A320客机以最快时间与最低燃油消耗为综合优化目标时的下降段进行轨迹优化,仿真实验验证,A320能够达到了指定下降高度与马赫数,且满足飞机物理性能与乘客乘坐体验,为优化A320客机下降段轨迹提供了有效的解决方案。
参 考 文 献
[1]王宏志.基于遗传算法解决飞机优化爬升问题研究[D].西安:西北工业大学,2005.
[2]朱思斌,李瑰贤,韩俊伟.基于改进微粒群算法的飞机纵向飞行轨迹优化[J].江南大学学报(自然科学版),2012,11(02):163-168.
[3]王宇,杨振博,余雄庆,柴啸.考虑风场、雷雨区的下一代客机轨迹多目标优化[J].航空计算技术,2019,49(02):19-23.
[4]宋乐,赵淑利.以飞行成本最优为目的的大型飞机的性能优化[J].兵工自动化,2009,28(06):43-45.
[5]刘航,仇国庆,刘平,杨金凤,周慧.带时间延迟工业最优控制问题扩展控制变量参数化算法[J].高校化学工程学报,2020,34(05):1283-1289.
[6]石博文. 基于控制变量参数化方法的发酵过程补料控制[D].江南大学,2020.
[7]仲维锋. 基于控制变量参数化的列车节能运行优化[D].北京交通大学,2019.
[8]方振平.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社, 2005.
[9]ZHANG Y H , YAN B B , MEMON A. A novel deep learning framework : Prediction and analysis of financial time series using CEEMD and LSTM [J]. Expert Systems With Applications , 2020 , 159 : 24-35.