玻璃与索网组合幕墙结构的静力性能分析与参数优化研究

玻璃与索网组合幕墙结构的静力性能分析与参数优化研究

蒋飞

上海欣世纪幕墙工程有限公司  上海市  201101

摘要：本文对玻璃与索网组合幕墙结构在不同参数条件下的静力性能进行了详细研究。研究表明，玻璃面板厚度的增加显著提升了结构刚度，减少了节点位移和拉索挠度；拉索截面尺寸和纵索预拉力的优化有效提高了结构的抗变形能力；合理的玻璃分割尺寸设计则显著降低了玻璃面板和拉索的内力与应力。本研究为索网组合幕墙的设计与优化提供了科学依据，并对实际工程应用具有指导意义。

关键词：静力性能、有限元分析、结构优化

1 引言

在现代建筑工程中，索网幕墙因其独特的轻质与通透特性，广泛应用于大型公共建筑和高层建筑的外立面设计。然而，由于其结构的柔性特征，索网幕墙在外部荷载特别是风荷载作用下表现出显著的几何非线性和大变形特点，给结构设计和性能评估带来了挑战。玻璃作为索网幕墙的主要组成部分，其厚度、分割尺寸等参数的变化，直接影响整个幕墙系统的刚度和稳定性。同时，拉索的截面尺寸和预应力水平也在一定程度上决定了幕墙的抗变形能力和承载性能。因此，研究索网幕墙在不同参数条件下的静力性能，对于优化设计方案、提高结构安全性具有重要的理论和实际意义。

2 SAP2000 有限元模型的建立

2.1 构件形式

在运用SAP2000软件进行结构工程的建模与分析时，首要步骤是精确设定材料的物理与力学特性，这涵盖了拉索、玻璃面板及不锈钢驳接爪件等关键组件。针对不同应用场景下构件参数的多样性，我们进行了详尽的模拟分析。

对于玻璃面板，考虑了六种不同厚度（8mm、10mm、12mm、14mm、16mm、18mm）的模型，以评估其对整体结构性能的影响。同时，拉索的直径也设定为一系列值（10.8mm、14mm、18.2mm、22.5mm、28mm、30.5mm），以探索直径变化对结构稳定性的贡献。此外，统一采用100系列不锈钢驳接爪件，以确保连接部件的标准化与一致性。设定拉索的弹性模量为1.35×105 MPa，该值反映了高强度钢材的典型力学性能；玻璃面板的弹性模量则设为0.72×105 MPa，体现了玻璃材料的刚度特性；不锈钢驳接爪件的弹性模量高达2.06×105 MPa，彰显了其优异的抗变形能力。设定驳接爪与钢拉索均为0.3，而玻璃面板则为0.2，这些值对于精确计算材料的横向变形至关重要。设定钢拉索与不锈钢爪件的线膨胀系数为1.2×10-5，玻璃面板线膨胀系数为0.9×10-5。预应力拉索与不锈钢爪件重力密度均为78.5 KN/m³，玻璃面板的重力密度则为25.6 KN/m³，以反映材料间的质量差异。

基于上述参数设置，我们构建了相应的模型（如图1-2所示），并进行了深入的模拟分析，以期为实际工程设计提供科学依据和参考。

图1 有限元模型的设计示意图

图2 （a）有限元建模模型图；（b）有限元计算模型图

2.2 工况的模拟方法

定义材料属性后，对拉索施加预应力是至关重要的一环。实现预应力加载的策略多样，本文特选用了降温法作为施加预拉力的方法。该方法首先明确所需的预拉力目标值，随后通过计算得出相应的温度调整量。在SAP2000的数值模拟流程中，这一温度调整量被作为温度荷载施加于拉索上，从而间接实现预拉力的有效施加。

3 参数对索网幕墙静力性能的影响

3.1 玻璃面板的厚度的影响

本研究聚焦于单一变量——玻璃面板厚度的调整，在维持索结构横截面尺寸恒定、纵横向索预应力均衡以及玻璃面板划分模式固定的实验框架下实施。具体而言，我们设定了六个厚度梯度，分别是8 mm、10 mm、12 mm、14 mm、16 mm及18 mm，以探究其对系统性能的影响。同时，为确保实验条件的一致性，预应力索的直径被标准化为22.5 mm，玻璃面板的分割规格锁定为1.5 m×1.2 mm，且钢索的预加张力保持在160NM的稳定水平。通过细致计算，我们获取了不同玻璃厚度下拉索最大挠度及节点最大位移的详尽数据，并将这些关键指标整理于表1中，为后续深入分析与讨论奠定坚实基础。

图3描绘了玻璃面板厚度的变化对玻璃面板最大内力/应力、纵横索最大应力、拉索最大挠度及节点最大位移之间的影响。这些图表不仅为理解结构响应提供了直观依据，也为后续的优化设计与性能评估奠定了坚实基础。

表1 玻璃面板厚度变化的影响

图3 玻璃面板厚度变化对结构性能的影响

深入分析结果显示，玻璃面板厚度的调整对纵索内部应力的影响显著超过横索，这主要归因于纵索在结构中的承重主导地位。为了进一步厘清这一变化规律，我们针对玻璃面板厚度变化时索网玻璃幕墙中拉索内力的演变进行了深入研究，并将拉索最大内力的变动趋势以图4的形式直观呈现。在此，我们设定了六个不同的工况，以玻璃面板厚度的递增（8mm至18mm）作为区分标准，分别标记为工况1至工况6。这一划分不仅便于数据分析，也清晰地反映了玻璃面板厚度变化对拉索内力特性的具体影响。

图4 不同工况下拉索最大应力变化情况

由图3和图4可知，随着玻璃面板厚度的递增，整体结构体系的性能展现出显著的变化趋势。具体而言，玻璃面板的内力呈现出较为明显的增长态势，其增长模式接近线性，表明厚度增加直接提升了面板的承载能力。同时，玻璃面板的最大应力却呈下降趋势，这归因于厚度增加导致的截面面积增大，进而分散了应力集中现象。

另一方面，纵索与横索的最大应力均略有上升，但增长趋势并不显著。值得注意的是，拉索体系中的最大内力发生在纵索的中部，且该位置恒定于2.4m处，这可能与结构的几何布局及受力特性有关。

进一步细致分析揭示，随着玻璃面板厚度的逐步增加，索网结构的最大节点位移以及纵横索的挠度均展现出明显的缩减趋势。这一现象背后的原因在于，增厚的玻璃面板显著增强了整体结构的刚度，进而削弱了其原有的柔性，有效限制了结构在受力作用下的位移与挠度变化。值得注意的是，横索挠度的减少幅度相较于纵索更为显著，这或可归因于横索通常具有较大的跨度且数量配置相对较少，使得结构在横向维度上的初始刚度相对较低，因此，在面板厚度增加时，该方向的刚度改善效果尤为突出。

3.2 横索截面变化的影响

为了探究幕墙结构在拉索截面尺寸调整下的响应特性，我们设计了一项实验，通过改变索的直径来实现。在构建分析模型时，我们设定了恒定的风荷载条件，即风荷载值为1KN/m²，以确保实验的一致性和可比性。实验分为六个独立的工况，分别对应不同的横索直径设置：10.8mm、14mm、18.2mm、22.5mm、28mm及30.5mm。同时，为控制其他变量，我们固定了玻璃面板的厚度为12mm，并保持玻璃面板的划分尺寸为1.5m×1.2m不变。

通过详尽的计算分析，我们获得了拉索截面变化对整体结构体系影响的数据集，并将这些结果整理在表2中，以便后续深入解析。为了进一步直观展示各变量之间的关联性和变化趋势，我们绘制了一系列图表，如图5所示，这些图表清晰地描绘了不同工况下结构体系性能的变化关系。

表2 横截面变化时结构性能

图5 横截面变化对结构的影响

由表2可知，横索直径的调整导致了多项性能指标的细微但显著的下降，各指标变化幅度各异。随着横索直径及其横截面面积的变化，玻璃面板的内力和应力均呈现出微弱的减小趋势，这一现象表明横索直径的微调对玻璃面板的性能影响甚微，可视为可忽略因素。

此外，纵索与横索最大挠度随横索直径变化而减小的现象。值得注意的是，横索最大挠度的减小幅度相较于纵索更为显著，这暗示了横索直径的变化对横索自身挠度特性的影响更为直接和显著，体现了横索在整体结构中的特定作用与敏感性。综上所述，横索直径的调整虽然对玻璃面板性能影响有限，但在优化索网结构挠度性能方面展现出了一定的潜力。

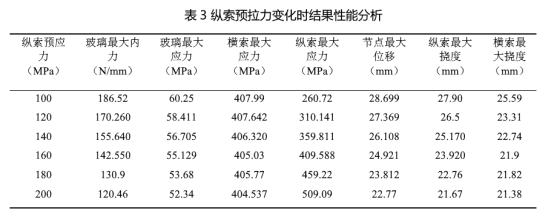
3.3 纵索预拉力变化的影响

在保持玻璃面板所受荷载恒定，并设定玻璃面板厚度为12mm、尺寸为1.5m×1.2m，以及钢索直径为22.5mm的条件下，我们构建了多个有限元数值模型，其中拉索预应力分别设定为100KN、120KN、140KN、160KN、180KN及200KN。

纵索预拉力变导致结构性能变化如表3所示。进一步绘制了详细的变化规律图（见图6），图中清晰呈现了玻璃面板力学性能、结构挠度及索应力随拉索预应力调整的动态响应，为深入理解索网幕墙结构的性能调控机制提供了有力支持。

图6拉索预拉力变化对结构的影响

上述数值计算模型分析揭示了索网玻璃幕墙在拉索预拉力增强过程中的性能变化特征。随着拉索预拉力的提升，玻璃面板的内力显著下降，表明预拉力的增大有效分散了面板上的荷载作用。同时，玻璃面板的应力亦有所减小，尽管减小趋势相对平缓，但这反映了结构体系整体刚度的增强。值得注意的是，横索的最大应力虽有所减小，但变化不显著，而纵索的最大应力则呈现出较为明显的增加趋势，且增幅较大，这揭示了拉索预应力调整对纵索力学状态的影响更为显著，相比之下，横索的变化可视为次要，因此在检测时可优先考虑对纵索的性能进行评估。

此外，分析还表明，无论是纵索还是横索，其最大挠度均随预拉力的增加而显著减小，显示出结构变形能力的降低。特别地，横索挠度的减小幅度初期较大，随后逐渐放缓，而纵索挠度则展现出近似的线性减小关系。尽管两者最终减小值相近，但这一过程中纵索挠度的变化模式更为直接。同时，结构体系最大节点位移的显著减小也进一步印证了拉索预应力对节点位移的显著影响，凸显了预应力调整在提升结构稳定性方面的关键作用。

3.4 玻璃分割尺寸的影响

实验中，六种不同的玻璃面板分割尺寸：2.25×1.2m、1.8×1.2m、1.5×1.2m、1.125×1.2m、1.0×1.2m及0.9×1.2 m，以探究尺寸变化与结构性能的关联。所有工况中，钢索的预应力统一设定为1602KN，纵横索直径22.5mm，玻璃面板厚度12mm。通过数值模拟与数据分析，获得了不同工况下的关键性能指标，如表4所示。

图7了展示玻璃面板分割尺寸与结构性能之间的动态关系。

表4 不同分割尺寸对结构的影响

图7 玻璃分割尺寸对结构的影响

图8展示了不同玻璃面板分割尺寸下钢索最大内力的变化情况。

图8 不同分割尺寸对拉索最大内力的影响

玻璃面板分割尺寸的变化对结构整体性能产生了显著影响。具体而言，随着分割尺寸的减小，玻璃板的最大内力与应力均呈现大幅降低趋势。此外，钢索的最大应力减小，但变化幅度相对较小，且纵向承重索的减小更为显著，如图3-8所示，拉索最大内力在分割尺寸为2.4m处集中显现。

此外，节点最大位移随分割尺寸减小而减少约40%，反映出结构整体刚度的大幅提升与柔性的相应降低。纵横拉索的最大挠度亦呈现显著下降趋势，其中纵向挠度减小尤为突出，达到约47%，而横向挠度减小约32%。这些发现强调了玻璃面板合理分割对于优化结构性能的重要性，在实际应用中需予以充分考虑。

4 本章小结

本文通过有限元模型对玻璃与索网组合幕墙结构在不同参数条件下的静力性能进行了系统研究。结果表明：

（1）玻璃面板厚度的增加显著提升了幕墙结构的整体刚度，降低了节点最大位移和拉索的最大挠度，同时增强了结构的抗风性能。然而，玻璃面板厚度的增加对纵横拉索的内力影响较小。

（2）拉索截面尺寸的增大对玻璃面板内力和应力的影响较为有限，但显著降低了纵横拉索的最大挠度，优化了索网幕墙的柔性特征，从而提高了结构的稳定性。

（3）纵索预拉力的提升有效减小了玻璃面板的内力与应力，并显著降低了纵横拉索的最大挠度和节点最大位移，表明合理的预应力设置对于增强结构刚度、提高抗变形能力至关重要。

（4）玻璃分割尺寸的减小显著降低了玻璃面板的内力与应力，同时减少了纵横拉索的最大挠度和节点最大位移。这一结果表明，适当的玻璃分割尺寸设计能够有效提升索网幕墙的整体结构性能。

参考文献

[1]张杰,吕令毅.点支式玻璃幕墙系统耦合动力分析[J].建筑技术开发,2002,(05):5-6+9.

[2]种迅,李一松,蒋庆,等.某塔楼玻璃幕墙结构模型试验研究及有限元分析[J].建筑结构,2021,51(03):71-76.

[3]张瑜.单层平面索网幕墙力学性能分析[D].沈阳工业大学,2014.

[4]王永慧.单层平面索网点支式玻璃幕墙结构性能研究[D].昆明理工大学,2009.