（重庆巴川国际）
摘要：简谐振动基本数学原理是简谐振动现象的最直观解释，学习物理应是由现象到本质属性追求的一个过程。在长期的物理探索中，人类对已知世界现象规律的逐步探索已经累计到了一个量的高度，科学追求的未来世界是逐渐由未知到绝大部分已知的转化。本次推导着重引用三角函数的求导与物理意义的结合。
（附注：
）
关键词：简谐振动 三角函数求导 虚圆 绝对参考系
一﹑简谐振动运动本质
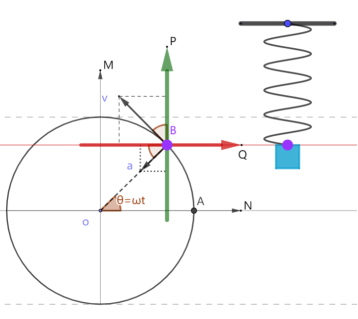
图1
上图为水平面上匀速圆周运动与弹簧振子的关联运动。由此可见二维简谐振动是建立在研究匀速圆周运动基础上，针对一维方向的运动研究。
匀速圆周运动要点回顾：匀速圆周运动从位移（x）﹑速度（v）﹑加速度（a）三个矢量考虑其性质。这里的位移主要考虑AB
位移大小方向均发生变化；速度大小不变，方向与向心加速度方向保持垂直；向心加速度大小不变，方向指向圆心。
本次探讨以ON为x轴正方向，以OM为y轴正方向。分别在静止的o点，以及运动的B点建立直角坐标系。如图1所示B点位置在以o点为原点的直角坐标系的一象限；速度在以B点为原点的直角坐标系的第二象限；加速度在以B点为原点的直角坐标系的第三象限。
维度分析：
x轴 | y轴 | |
位移（x） |
|
|
由 | ||
速度（v） |
|
|
一阶导数物理意义 |
|
|
加速度（a） |
|
|
二阶导数物理意义 |
|
|
|
|
|
总结：考虑绝对值 
，
二﹑简谐振动能量情况：
x轴动能与势能：
即
同理可得
y轴动能与势能：
即
由此可见，水平面匀速圆周运动结合的简谐振动可以看出一维情况下势能与简谐振动公式
相符合，而动能由另一个维度的动能来担当。
三﹑简谐振动的实例情况单摆：
①悬点：固定。
②摆球：直径远远小于摆线长度且质量大。
③细线：质量不计﹑细线不可伸长
④摆角：摆线与中心线的夹角小于5°
⑤其他因素：忽略空气阻力
图2
（注：夹角
）
如图建立自然直角坐标系，即以摆球运动方向为x轴，垂直与运动方向为y轴建立直角坐标系。切线方向G1改变速度大小，法线方向G2。当夹角
，理想化模型下将G1近似处理为水平方向简谐振动的回复力，且OA=l，AB=x。
由简谐振动
且
则
即重力加速度：
或
四﹑总结：理解一维简谐振动的理解应借助与之对应的二维匀速圆周运动，即可以理解为简谐振动是存在一个虚圆运动。表达式：
即简谐振动频率f与匀速圆周运动的圆频率相一致。
物理学与数学联系非常紧密，他们相辅相成。每一个物理现象的背后我们应尽可能的找到其与之对应的数学含义，用以更好的解释物理规律背后的本质。
参考文献：高中物理人教版选择性必修第一册第二章机械振动。
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网(www.qikanchina.com) 琼ICP备2021005105号
即
A
