国家电投集团甘肃分公司酒嘉维检中心,敦煌 736200
摘要:光伏发电量预测是光伏电站可研、建设及运维中的重要环节,为了提高发电量评估的准确性,通过在传统计算公式的基础上增加温度修正因子, 以一年的实测气象数据及组件发电量数据为基础,通过对多个发电预测算法计算结果进行分析比较,结果表明:通过拟合法引入温度修正系数及常量后,全年发电量预估值更接近实测数据, 发电量预测准确度显著提高。
关键词:光伏发电;背板温度;发电量预测;拟合;准确度;
引言
近十年来,太阳能作为绿色无污染的可再生能源在我国得到了规模化长足发展。然而,在项目投资过程中,很多投资方未对建设地区的电站发电量进行准确科学的评估和预测,只是盲目遵循大流,电站实际发电量和预测结果相差巨大,导致投资收益出现重大偏差。目前,光伏电站在发电量预测中仅简单引入辐照度的影响,而在实际运行中,作为影响光伏系统发电量另一重要因素的太阳电池温度,却被忽略或仅凭理论经验估算。本文采用现场太阳能发电系统实测数据,分析比较了不同发电量预测算法的计算差异,论证了引入温度拟合修正的发电量预测方法的准确性。
1 实验原理
1.1实验目的
光伏电站设计者在做电站发电量预测分析时,往往只考虑当地辐照度水平和部分理论损失,所得到的可研发电量理论值和实际运行后的真实值存在较大偏差。在实际过程中,太阳电池组件温度对发电量会有较大影响,而这部分影响由于相对复杂往往被忽略或用经验参数代替。为更准确的衡量太阳电池组件温度对发电量的影响,进而实现光伏电站理论发电量精确预测,本研究考虑在实际工况条件下连续对实验光伏系统组件直流输出功率进行完整一年的运行数据研究,分析论证了光伏系统在运行过程中温度变化对光伏组件发电能力的影响,得出更适用于光伏电站发电量可研计算的方法与公式。
1.2实验设计及设备
实验采用单晶硅组件构成的系统,组件数量为10块,组件为厂家特别定制,每块都经过室内STC功率测试,阵列容量为2.864kW,具体参数见表1。阵列安装时在安装前进行外观测试和EL隐裂测试,确保安装的组件无任何外观和隐裂缺陷,为模拟电站正常运维,减少灰尘和污渍对发电量的影响,每十五天对阵列进行一次清洗,并在极端天气如沙尘暴后进行及时清洗;背板温度贴片在安装时,选择阵列中心位置的一块组件,按照IEC 61853-1-2011[1]中的要求,设置3个温度采集贴片,并随机挑选其他两块组件的中心位置各设置1个背板温度采集贴片。
表1 系统参数
Moudle-size:(m) | Pmax:(W) | γ (%/℃) | Efficiency:(%) | |
1.65*0.99 | 2864 | -0.0041 | 17.53% | |
环境采集装置中,测光单元采用荷兰kipzon公司高端辐射表CMP21,准确度为±2%,空气温度采集单元为美国Cambell的109空温传感器,准确度为±1℃,背板温度采集单元为欧米伽公司的T42热电偶,准确度为±1℃;电性能采集装置中,电压和电流传感器分别采用准确度优于±0.5%的国内某军工企业的电压电流传感器 ;数据汇总采集单元为美国Cambell公司生产的CR3000宽温数据采集器,采集精度<0.02%。系统简图见图1

1.3数据采集方式
使用该系统进行为期一年的连续监测,采集辐照度,功率(DC端数据),电池温度,空气温度,得到一年的实验数据,数据格式如表2所示。
表2 系统采集原始数据
Time | Irradiance (W/㎡) | Power(W) | Tair (℃) | Tcell (℃) |
2021/3/1 9:08 | 139.2 | 338.8 | 5.0 | 8.7 |
2021/3/1 9:09 | 160.7 | 390.1 | 5.1 | 9.0 |
┊ | ┊ | ┊ | ┊ | ┊ |
2022/2/28 18:51 | 128.7 | 325.5 | 9.1 | 10.9 |
2022/2/28 18:52 | 122.4 | 309.2 | 9.0 | 10.9 |
2.传统预测方法的弊端
2.1传统发电量预测方法与实测值的偏差
常规电站可研报告中发电量预测方法仅引入辐照度,计算时只需该地区的辐射数据,即可得出该地区一年的发电量,计算方式如下:
![]() (1)
(1)
式中,Y1—系统发电量; G—光伏组件平面接收的辐照度;Pstc—系统额定功率。
为了增加预测准确率,本计算过程中带入的原始数据为分钟数据,将累积辐照度值带入公式(1),从而累积得出全年的发电量预测值,并按季度区分,计算结果见表3
表3传统发电量预测方法与实测值的偏差
时间间隔 | 全年 | 春季 | 夏季 | 秋季 | 冬季 |
Y1(kW·h) | 5454.00 | 1470.95 | 1489.73 | 1329.11 | 1164.21 |
实测发电量(kW·h) | 4894.80 | 1316.59 | 1310.35 | 1184.16 | 1083.69 |
两者偏差(%) | 11.4 | 11.7 | 13.7 | 12.2 | 7.4 |
由上表可以得出,用传统发电量预测方法计算的全年发电量预测值与实测值之间的偏差高达11.4%, 如果引用该值作为科研理论发电值,会导致可研分析偏大,过高的评估了当地的发电量水平,导致投资方不能准确评估电站收益水平,造成较大经济损失。
2.2预测发电量与实测值偏差过大的原因分析
为了提高传统发电量预测方法的准确性,对预测发电量与实测值偏差过大的原因进行分析,影响光伏组件发电能力的因素主要包括环境因素和组件因素,其中环境因素主要包括阴影遮挡、沙尘积灰、污渍、降雪、降雨以及环境温度,而组件因素主要包括组件失配性、组件初始光衰、组件表面反射损失、直流端线损。
本实验所采用的系统,在搭建之初,严格按照系统设计及检测相关标准,对部分损失进行了规避:
1)光伏系统前方无遮挡故无阴影损失;
2)光伏系统所处检测位置在荒漠戈壁,无大量飞禽,无鸟类遗粪导致的功率损失;
3)数据分析时剔除了辐照度为120W/㎡以下的发电量数据和环境数据,规避了降雨天气、降雪天气、沙尘暴天气及其他低辐照度时导致发电量损失及发电能力不稳定的情况;
4)在极端天气如大雪、沙尘暴天气后,会进行阵列清洗,所以该系统极端天气后导致的直流端功率损失可忽略不计;
5)逆变器安装在阵列支架后,直流线缆距离较短,线损可忽略不计;
6)所用组件为厂家特别定制,每块之间的工作电流值偏差低于0.1%,组件失配性可忽略不计。
对其他损失分析如下:
7)灰尘影响
灰尘导致的损失主要因为组件表面玻璃上自然灰尘的不断积累和人为废气污浊物的附着,导致进入组件的太阳辐射量降低,影响光电转换效率[3],研究结果表明,在降雨量少的地方由于灰尘导致的功率损失可以达到15%[3,4],为了降低本实验中沙尘对直流端发电性能的影响,采用了十五天进行一次清洗的周期清洗方式,并实地通过使用IV功率测试仪周期跟踪测试,结果表明无降水天气十五天的灰尘影响极值为5.3%,为了均衡每天沙尘的影响,并考虑降雨天气导致灰尘影响降低的现象,结合其他类似研究结果,此处采用经验值2%[5]。
8)温度影响
光伏组件的最大功率测量是在STC条件下对电压-电流特性的测量,组件的光电转换效率也通过该值计算得出,电能产出的多少取决于组件表面接收的辐射量,接收的辐射量一部分转换为电能,一部分会转换为热能[6,7],从而导致部分可利用光能的损失,故组件的光电转换效率会随着电池温度的升高减少,研究表明,以STC功率为参考标准,组件因温度损失而导致的发电量最高可达到14.5%[8],组件温升导致的损失是多个因素导致的,损失值会随着地域和气候而发生较大变化,本文重点论证了组件电池温升导致功率损失对预测发电量的影响并给出了修正方法与公式。
9)组件初始光衰损失
光伏组件功率衰减是指随着光照时间的增加,组件输出功率不断呈下降趋势的现象[9]。组件功率衰减直接关系到组件的发电效率,组件功率衰减包括组件初始光致衰减、组件材料老化衰减及外界环境或破坏性因素导致的组件功率衰减[10],研究表明光伏组件初始都有光致衰减现象,但不同批次功率衰减幅度差异较大,1%~3.7% 都有,因此改善初始光致衰减现象显得非常必要[11]。本实验中涉及到组件的初始光衰采用该最低经验值1%。
10)组件表面反射损失
组件将吸收的太阳能转换为电能过程中,会有一定量的太阳辐射从组件表面反射回大气,这部分能量的损失称为反射损失[3].可以通过在组件表面镀减反膜来减少这部分的损失,本实验未采用镀膜组件,反射损失采用其他研究中的经验值2%。
3 新方法的论证与分析
为了提高预测发电量值的准确度,在传统发电量预测方法的基础上,对传统公式进行改进与论证,分别带入了灰尘影响、组件初始光衰影响和组件表面反射损失影响,并重点论证了组件电池温温度对预测发电量的影响,从而产生了新的预测方法。
3.1引入NOCT温度修正的传统发电量预测方法
IEC 61215-2009 中规定NOCT的测试条件为光伏电池在辐照度800W/㎡、环境温度20℃、风速1m/s条件下的温度,NOCT模型主要是为了预测太阳能电池工作温度,该方法认为光伏电池的工作温度与环境温度之差与太阳辐射成线性关系,据此计算就得到光伏电池的实际工作温度。通过获取NOCT值,在传统发电量预测方法计算公式上加入背板温度的修正,从而引入温度的影响,使预测值更科学合理,计算方式如下:
![]() (2)
(2)
式中,Y1—系统发电量;K1—灰尘影响经验系数2%;K2—初始光衰损失经验系数1%;K3—组件表面反射损失经验系数2%;G—光伏组件单位面积接收的辐照度;Pstc—系统额定功率;![]() —组件功率温度系数;
—组件功率温度系数;![]() =45℃。
=45℃。
将辐照度数据带入公式2,积分得出全年的发电量预测值,计算结果见表4
表4公式(2)全年及分季节预测值
时间间隔 | 全年 | 春季 | 夏季 | 秋季 | 冬季 |
Y2(kW·h) | 4756.43 | 1282.82 | 1299.19 | 1159.12 | 1015.31 |
3.2引入平均温度和平均组件温度的发电量预测方法
上述NOCT温度实际上是标准中规定的光伏组件处于某一特定条件下的静态温度状况。而在实际工况中,不同区域的气候差异,以及组件温度时刻随环境变化产生的动态差异并未进行考虑。因此通过实际测量将全年环境温度平均值以及全年电池温度平均值对公式(2)进行修正,得出公式(3),能够更准确的对组件发电值进行计算。
![]() (3)
(3)
式中:![]() 为时间间隔内的电池温度平均值,
为时间间隔内的电池温度平均值,![]() 为时间间隔内的空气温度平均值
为时间间隔内的空气温度平均值
对得到的全年数据首先进行数据筛选,剔除辐照度低于120w/m2的所有数据,剔除系统停电期间的数据,剔除其他错误无效数据,对发电量,辐射量数据求和,对其他数据取平均值,得到各季节和全年的数据整合表,见表5。
表5 实测环境数据
时间间隔 | 实测发电量 | 实测辐射量 | 平均空气温度 | 平均电池温度 |
/ | kW·h | kW·h/m2 | ℃ | ℃ |
春季 | 1316.59 | 513.65 | 18.02 | 30.60 |
夏季 | 1310.35 | 520.20 | 30.56 | 43.95 |
秋天 | 1184.16 | 464.12 | 15.15 | 28.01 |
冬天 | 1083.69 | 406.53 | -0.26 | 12.96 |
全年 | 4894.80 | 1904.50 | 17.00 | 30.01 |
将表5中的春夏秋冬及全年分别带入公式(3),累积得出各季节及全年的发电量预测值,计算结果见表6
表6公式(3)全年及分季节预测值
时间间隔 | 全年 | 春季 | 夏季 | 秋季 | 冬季 |
Y3(kW·h) | 4935.93 | 1333.71 | 1346.01 | 1191.64 | 1052.63 |
3.3 引入温度拟合修正的发电量预测方法
辐照和电池温度是影响光伏发电量的两大主要因素,而这两个因素存在一定的关联性,通过大量试验样本拟合得到两者的关联公式,能够更进一步提高发电量预测方法的地域适用性和结果的准确度。
通过对实测数据进行分析筛选,剔除非工况情况的数据,如停电检修、阴雨天气以及低于120W/m2的低辐照度数据,用筛选后的有效数据做四季及全年电池温度与辐照度关系图,然后进行曲线拟合,得到西北地区电池温度与辐照度相关性的图表及曲线函数。
3.3.1 春季电池温度与辐照度相关性
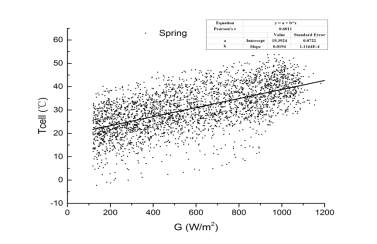
图2 春季电池温度与辐照度关系图
由图2可以得到春季电池温度与辐照度的线性拟合函数:Tcell=0.0194*G+19.392,将其与公式(3)相结合,从而得到引入电池温度后新的春季发电量计算公式:
![]() (4)
(4)
将每分钟辐照度平均值和空气温度平均值带入公式,累积得出春季的发电量预测值,经过计算,Y4=1321.09 kW·h。
3.3.2 夏季电池温度与辐照度相关性

图3 夏季电池温度与辐照度关系图
由图3可以得到夏季电池温度与辐照度的线性拟合函数:Tcell=0.0227*G+30.826,将将其与公式(3)相结合,从而得到引入电池温度后的夏季发电量计算公式(5):
![]() (5)
(5)
将每分钟辐照度平均值和空气温度平均值带入公式,累积得出夏季的发电量预测值,经过计算,Y5=1332 kW·h。
3.3.3 秋季电池温度与辐照度相关性

图4 秋季电池温度与辐照度关系图
由图4可以得到秋季电池温度与辐照度的线性拟合函数:Tcell=0.0282*G+10.651,将其与将其与公式(3)相结合,从而得到引入电池温度后的秋季发电量计算公式(6):
![]() (6)
(6)
将每分钟辐照度平均值和空气温度平均值带入公式,累积得出秋季的发电量预测值,经过计算,Y6=1190.23 kW·h。
3.3.4 冬季电池温度与辐照度相关性
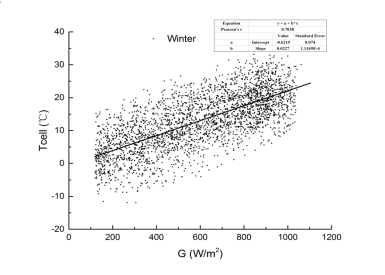
图5 冬季电池温度与辐照度关系图
由图5可以得到冬季电池温度与辐照度的线性拟合函数:Tcell=0.0227*G-0.6215,将其与公式(3)相结合,从而得到引入电池温度后的冬季发电量计算公式(7):
![]() (7)
(7)
将每分钟辐照度平均值和空气温度平均值带入公式,累积得出冬季的发电量预测值,经过计算,Y7=1041.57 kW·h。
3.3.5 全年电池温度与辐照度相关性

图6 全年电池温度与辐照度关系图
由图6可以得到全年电池温度与辐照度的线性拟合函数:Tcell=0.0218*G+17.117,将其与公式(3)相结合,从而得到引入电池温度后的全年发电量计算公式(8):
![]() (8)
(8)
将每分钟辐照度平均值和空气温度平均值带入公式,累积得出全年的发电量预测值,经过计算,Y8=4883.96 kW·h。
4 结果比对
以表3中的实测值为参考,按照公式(1)~(8)进行数据计算,分别对比传统发电量预测方法、引入NOCT温度修正的传统发电量预测方法、四种计算结果进行比较分析,分析结果如表4所示。
表4 不同计算方法的发电量预测值及与实测值偏差
时间间隔 | 实测电量 | Y1 | 偏差 | Y2 | 偏差 | Y3 | 偏差 | Y(4-8) | 偏差 |
/ | kW·h | kW·h | % | kW·h | % | kW·h | % | kW·h | % |
全年 | 4894.80 | 5454.00 | 11.4 | 4756.43 | -2.8 | 4935.93 | 0.8 | 4883.96 | -0.2 |
春季 | 1316.59 | 1470.95 | 11.7 | 1282.82 | -2.6 | 1333.71 | 1.3 | 1321.09 | 0.3 |
夏季 | 1310.35 | 1489.73 | 13.7 | 1299.19 | -0.9 | 1346.01 | 2.7 | 1332.00 | 1.7 |
秋天 | 1184.16 | 1329.11 | 12.2 | 1159.12 | -2.1 | 1191.64 | 0.6 | 1190.23 | 0.5 |
冬天 | 1083.69 | 1164.21 | 7.4 | 1015.31 | -6.3 | 1052.63 | -2.9 | 1041.57 | -3.9 |
通过比较发现:
(1)采用传统发电量预测方法计算的发电量与实际值偏差达到11.4%,该方法对项目工程投资经济测算带来的误差较大,并不适合准确的对项目发电量进行评估。
(2)采用NOCT温度修正的传统发电量预测方法计算的发电量与实际值偏差为-2.8%,处于工程投资可容许范围之内,但是该方法依据标准将NOCT值直接修正至STC下的25℃,没有考虑不同区域温度的差异性,通过该计算方法计算的发电量预测值在不同区域会存在明显差异;
(3)采用平均温度和平均组件温度的发电量预测方法和温度拟合修正的发电量预测方法所计算的发电量与实际值之间的偏差分别为0.8%和-0.2%,都在1%以内更接近实际值,充分证明了温度对发电量预测精确性的影响。
5 结论
5.1组件温度对发电量影响极大,引入温度拟合修正的发电量预测能够更准确的预测光伏电站发电量,能够为项目可行性研究提供更准确的投资参考。
5.2在实际工程应用中,如不能对现场进行长期的环境参数测量,也可以采用公式(3)的计算方法,预测结果也能达到工程应用要求。
5.3 由于一年中不同时段,环境温度变化差异较大,在发电量预测时为提高预测精度,可分月度或季度进行预测计算,能够得到更准确的结果。
参考文献
[1] 马志恒. 太阳能电池组件功率衰减分析[J]. 中国高新技术企业,2012,(17): 32 - 33.
[2] 林存超. 光伏组件质量问题分析及安装质量控制[J]. 中国科技信息,2015(01).
[3] 黄盛娟.光伏组件功率衰减分析研究[J].太阳能技术产品与工程科技信息,2015,(2): 204 - 205.