自制几何模型在高中数学教学中的实践

自制几何模型在高中数学教学中的实践

刘俊霞

开封市祥符高级中学

摘要　要实现学生由认识平面图形到认识立体图形的飞跃，并且还要逐步改变学生只习惯于在一个平面内考虑问题的状态，培养和发展学生的几何直观能力、运用图形语言进行交流的能力、空间想象能力和一定的推理论证能力。因此，我们考虑利用自制几何模型的演示来创设教学情景，激发学生兴趣，改善教学效果。

关键词　自制　几何模型　教学　实践

在整个高中数学学习阶段，必修二第一章 空间几何体，第二章 点、直线、平面之间的位置关系，第四章第三节 空间直角坐标系及选修2-1中的第三章 空间向量与立体几何，这些章节都要求学生有较强的空间立体及抽象思维能力，学生在学习过程中普遍会感到比较困难。尤其是必修二中的前两章，在这两章中，不仅要实现学生由认识平面图形到认识立体图形的飞跃，并且还要逐步改变学生只习惯于在一个平面内考虑问题的状态，培养和发展学生的几何直观能力、运用图形语言进行交流的能力、空间想象能力和一定的推理论证能力。因此，我们考虑利用自制几何模型的展示来创设教学情景，激发学生兴趣，改善教学效果。

在教学中，我们发现，实物的形状一般只是比较近似于基本的几何形状，而这会给学生一种错觉，他们会认为概念中某些要求是可以忽略的，甚至是无关紧要的，它不仅会导致学生概念上的混淆，而且会影响学生养成严密思维的习惯；而有些几何关系，实物根本无法明确展示，而数学教学模型缺少的现状又是不能忽视的一个客观事实，我们几位老师就萌生了自制几何模型的想法并且付诸了实施，几何模型制作好后即投入到课堂教学实践，通过教学实践，我发现自制几何模型作为一种辅助的教学手段,的确可以起到很好的教学效果

一、以展为引，先展后讲

这种教学方式一般是用在概念型或结构特征的学习上，比如高中数学必修一第1.1.1节 锥、柱、台、球的结构特征，这节课的教学重点就是让学生感受大量空间实物及模型，概括出柱、锥、台、球的结构特征。在上本节课前，我会事先自制好一些锥体、柱体、台体、球体的模型，在上课开始即向学生展示这些模型，学生可以互相传看并触摸这些立体模型，相比课本上的图片展示，自制几何模型展示效果超级好。通过展示并让学生仔细观察，讨论各模型的结构特征，引导学生思考空间几何体的分类方法，提出适当的分类标准。而且对模型的全方位观察可以增强学生的直观感受，使学生充分感受锥体、柱体、台体、球体这几种空间几何体的整体结构，在此基础上，引导学生抽象概括出它们的结构特征。通过这些简单几何体的自由拼接，引导学生更进一步地讨论由这些不同的简单几何体组合而成的简单组合体的结构特征。

之所以如此安排本节课，是从学生的认识规律出发的，即先从整体上认识空间几何体，进行相应地分类后，再深入到细节，总结出其结构特征。

近几年的高考题多以多面体为载体直接考察线面位置关系，热点问题为平面的基本性质，经常考察线线、线面和面面关系的论证问题。在最初讲授这类问题时，我们通常把多面体放置在特定的正方体或球体内考虑，把题中涉及到的不规则的几何体转换放置在规则的几何体内，以分析其线条变化。看下面这些问题，如果有自制的模型做辅助，效果事半功倍！

例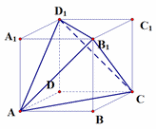 如：在正方体 中，设其棱长为 ．我们连接几条面对角线，如图，得到的几何体 为_____________（填名称），它的棱长为正方体棱长的___ __ 。在这里，你能发现正四面体的棱切球与正四面体以及正方体的关系了吧．

你的结论是：正四面体的棱切球的半径为_____（用正四面体的棱长 表示）．

附答案：正四面体 倍 正四面体的棱切球恰好为该正方体的内切球

这类题需要先让学生们思考、画出几何图形，然后再展示模型，加强与平面图形知识的联系，利用对比、引申、联想等方法，引导学生找出平面图形和立体图形的异同，以及两者的内在联系。

三、以展为辅，边展边讲

在大多数时间模型的利用是和讲述同步的，比如在讲到空间几何体的表面积与体积这一节内容时，教材一开始的思考是从学生熟悉的正方体和长方体的展开图入手，分析展开图与其表面积的关系，在这里，老师可以拿出事先准备好的正方体和长方体纸质模型，分别从不同的棱当场剪开，一边学生观察其展开图，一边老师介绍求几何体表面积的方法。然后老师拿出棱锥、棱柱、圆柱、圆锥、台体等几何模型，要求学生类比正方体和长方体得出其它几何体的表面积的求法。

空间元素位置关系的定性判断这类题型也是高考的常见题型，例如：

（2017·全国卷Ⅲ理·16）a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：

①当直线AB与a成60°角时，AB与b成30°角；

②当直线AB与a成60°角时，AB与b成60°角；

③直线AB与a所成角的最小值为45°；

④直线AB与a所成角的最大值为60°；

其中正确的是________。（填写所有正确结论的编号）

分析这道题时，我直接展示的相关几何模型，当对应的几何模型一展示，效果立竿见影，学生很快发现正确结论。

具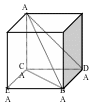 体的几何模型图已附在本文后面，在这里，我以构造如图正方体的形式来表达分析这道题

用EB表示a，BD表示b，当B在边BD上从D到B运动时，就会发现Rt△ABC位于Rt△ADC位置时，AB与BD垂直、与EB成45o­角，从D到B沿直线DB运动时，AB与BD所成的角在减小、与EB所成的角在增大，就会发现居于Rt△ABC位置时两角相等，且为60o­角，故选②③。

四、以制补展，深化理解

看到实物或模型，我们把这种空间几何体的问题转换为平面问题还是相对好理解的，而且我们最初接触立体几何也是遵循这种思路。但学习到一定程度的时候，就需要有逆向学习的能力，即给你平面图形，让你在脑子里形成立体图形，对于那些空间能力相对欠缺的学生可是不小的挑战，教材中有关空间几何体的三视图这一章节的难点即是根据所给三视图识别其所表示的空间几何体，在这个时候，我们用常规的展示模型法并不能让学生很好地理解实物的形象，这就需要学生们自己动手，进行自制、比对、拼接，形成符合题目要求的空间几何体。

例如：已知一个三棱锥的三视图如图所示，其中三个视图都是直角三角形，则在该三棱锥的四个面中，直角三角形的个数为

在遇到这种类型题时，对于那些空间想象能力还不足的学生，需要就地取材，用折纸的形式折出一个个符合三视图的三角形，然后通过拼接、移位、来理解由三视图所表示的空间几何体。通过这一节的学习和动手，可以进一步加强学生的空间想象力。

本文系2017年度河南省基础教育教学研究项目《自制几何模型在高中几何教学中的应用研究》（课题编号：JCJYC17030226）

【参考文献】

[1]张兴 朱全林 07 新课标高考立体明天我生日考点分面及解法探析.数学考试—高考专题突破（一）CN 54-1058/G4 2-1042，2018（2）

[2]郑永广，“多面体与球”问题的探索与集结，开封市祥符高中，2015.4

下面附一些我们自制模型的照片：