核心素养下小学生推理能力的案例研究

核心素养下小学生推理能力的案例研究

李年终

湖南省桃江县桃花江镇中心学校小学部 , 湖南 桃江 413400

摘要：小学数学核心素养中包括了对学生推理能力的培养，培养学生的推理能力是件非一蹴而就的事，这需要教师采取循序渐进的策略来培养学生的推理能力，这个循序渐进体现在从意识到能力的不断过渡和推进。具体来说，首先要通过培养学生层次分明的解题素养，类培养学生的逻辑推理意识；然后要通过运用思维导图向学生展示知识框架，以启发学生建立系统化、富逻辑性的知识掌握理念，来强化其推理意识；最后通过组织学生进行信息实验，通过对图形的探究来进行推理，以强化学生的推理能力。

关键词：小学数学；核心素养；推理能力

在核心素养这一教学概念的倡导和指引下，我们不仅对学生的培养有了更明晰的方向，对自身的教学方式创新也有了更多更重要的借鉴。在小学数学核心素养中就有对学生推理能力的培养要求，而且数学本身就是一门不滞于书本、以解决问题为主以及需要学生具备良好推理能力的学科，因之，让学生的思考活动充满逻辑性和科学性，即让学生具备良好的逻辑推理能力是至关重要的。教师要在培养学生推理能力上多增添一些关注，多下一些功夫。

一、解题层次分明，培养逻辑推理意识

培养推理能力，会经历一个长久的教学过程，首先要从培养学生的逻辑推理意识上下功夫。逻辑推理意识的养成是需要教师日积月累的引导才能逐步实现的。这一意识是需要教师在日常教学过程中有意对学生进行渗透的。鉴于数学是一门以解决问题为主的学科，数学的日常的教学内容基本上也是以解题教学为主的。因此，教师要把握好解题教学，在其中穿插进对学生逻辑推理意识的渗透。

逻辑推理意识是一种具有清晰思路、思考活动有条理和思维结构系统化这几方面特点的意识，根据其所具有的这些特点，教师在解题教学中，要做到讲解解题思路时让学生明白具备层次分明有条理的解题思路的重要性。具体来说，教师要为学生展示层次分明的解题过程，让学生在潜移默化中养成富有逻辑思考和层层推理的意识，继而养成逻辑推理意识。

例如：某工厂日均生产甲种零件360个，乙种零件的日均产个数比甲种零件多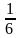 ，丙种零件的日均产个数占全部零件的日均产个数的 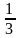，问该工厂一共生产零件多少个？

解题过程就要层次分明：乙种零件的日均产个数为甲种零件日均产个数的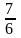 ，则乙种零件的日均产个数为36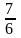0× =420；

由于丙种零件的日均产个数占全部零件的日均产个数的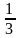 ，则甲、乙两种零件的日均产个数占全部零件的日均产个数的(1- )= ；

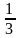则360+420=780（个）的数量占全部零件的日均产个数的 ，那么全部零件的日均产个数为780÷ =1170（个），则该工厂一共生产零件1170（个）。

总之，在解题教学中，思路清晰的解题过程是最为必要的。教师要在解题教学中为学生一步一步将之展示出来，以帮助学生养成有逻辑地分析和解决问题的习惯。进而帮助学生养成逻辑推理的意识。

二、运用思维导图，强化推理意识

在培养学生逻辑推理意识的基础上，就要着重强化学生的这种意识。强化学生的逻辑推理意识同样是一个长久的工作，应该渗透到日常教学中。数学对于学生掌握知识框架能力的要求是比较高的，因为数学解题中，通常不是考察的一个知识点，而是在一道题里面包含着多个知识点。对诸知识点进行融会贯通和系统掌握，是学生学好数学所应具备的良好素养。因此教师在帮助学生展示和掌握知识框架的时候，穿插对学生推理意识的强化工作。

在帮助学生整合知识体系的时候，思维导图是一种强力的辅助工具。思维导图是一种可以表达发射性思维的信息教学工具，它图文并重，能把某一数学知识体系中所包含的各分支知识点间的逻辑关系直观地展示出来。这样的知识脉络展示方式，通常能够强有效地辅助学生记忆和掌握整个知识体系。而且这样富有层理性和系统性的知识整合方式，也在向学生传达着从整体上掌握事物、用联系的观点看待问题、用推理的理念进行发散的良好理念，经常性地进行如此知识掌握活动，可以潜移默化地启发学生强化自身的逻辑推理意识。因此教师可以尝试在总结知识体系的教学活动中多运用思维导图这一强大工具，在帮助学生强化对知识掌握的同时，启发学生强化逻辑推理意识。

例如：在帮助学生梳理目前所学的小学数学中数与代数的知识体系时，笔者就运用思维导图将其用一棵树的图形在电子屏幕直观展示出来。首先在大树干“数与代数”上生出了四大知识分枝：数的认识、数的运算、式与方程以及比和比例，这四大知识分枝都各自生出下一级的其所包含的知识小分枝，就这样一级一级地向下延伸知识的“枝条”，最后构成一个结构鲜明的知识脉络，各部分知识分支的逻辑关系一览无遗。

通过思维导图，数与代数的知识体系被系统化且有逻辑性地直观展示出来，这潜移默化地强化了学生的逻辑思维意识。

三、进行信息实验，强化推理能力

在意识层面上有所进展后，就要着重在能力层面上寻求进展了。因此，在强化学生的逻辑推理意识之后，教师就要切实强化学生的推理能力。强化学生的推理能力，需要更进一步地引导学生进行推理活动。

在小学数学中，几何是一大主要内容，对几何图形进行直观想象和探究的过程，也伴随着逻辑推理活动的进行，因此，对几何图形进行探索的活动，也可以用来引导学生做思维的发散工作。

例如：在讲求圆柱体积时，笔者就引导学生从已学过的割圆术的角度来思考如何求圆柱的体积。我在电子白板中已经安装好的制图软件里插入圆柱体，然后让学生做等割重组的实验探究。有学生上来尝试，将圆柱体竖着等割为八份，重组后的图形变成了一个底面坑洼歪扭而近似于平行四边形的立体图形；之后陆续有学生上来进行展示，将圆柱体切割得越来越精细，重组的图形底面也越来越像一个平行四边形，甚至趋于矩形。于是学生推理到，如果继续以无限精细的切割法竖着等割圆柱体，则最后重组成的立体图形也就越来越接近一个长方体，而这个立体图形的高自然是原来圆柱的高，其底面积其实也就相当于原来圆柱体的底面积。于是，在自主信息实验探究中，学生进行了自主推理，这对于学生推理能力的强化有积极作用。

综上所述，对小学生推理能力的培养，并非一日之功，而是需要教师循序渐进地在培养学生逻辑推理意识和提高学生推理能力上稳步推进。在培养学生的推理能力时，教师切忌揠苗助长，而是要不断善加引导。其实在培养学生的推理能力上，还有很多种方法，也存在着很大的可挖掘空间。随着教学创新的不断深入推进，教师的教学方法也要紧跟脚步，不断改进革新。

参考文献

[1]赵丽. 基于核心素养下的小学数学逻辑推理能力培养[C]. 中国智慧工程研究会智能学习与创新研究工作委员会.2020年教育信息化与教育技术创新学术论坛（贵阳会场）论文集（五）.中国智慧工程研究会智能学习与创新研究工作委员会:重庆市鼎耘文化传播有限公司,2020.

[2]张琳珠.借助信息技术发展推理能力[J].基础教育论坛,2020(08)