多力共点的动态平衡问题处理方法探析

多力共点的动态平衡问题处理方法探析

李明哲

福建师范大学附属中学 350007

摘 要：超过三个共点力的多力动态平衡问题用常规的解析法较为复杂，本文通过分析两道多力动态平衡的问题，提出基于“矢量三角形法”的“矢量多边形法”来解决此类问题，具有直观、快速的优点.

关键词：共点力动态平衡；多边形法则；图解法

物体的动态平衡问题是高考命题的热点之一，常见的动态平衡问题是基于三力平衡进行设计，此类问题的解决思路通常有解析法、动态三角形法和相似三角形法. 通过适当的训练和总结，学生一般能够较好地掌握这类的问题的处理方法. 但对于超过三个共点力作用的动态平衡问题，对学生要求更高，需要有更灵活的技巧和运用数学解决物理问题的能力. 本文通过分析两道例题，指出解决多力动态平衡问题的解题技巧.

一、例题分析

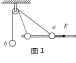例1 如图1所示，光滑的轻滑轮通过支架固定在天花板上，一足够长的细绳跨过滑轮，一端悬挂小球b，另一端与套在水平细杆上的小球a连接. 在水平拉力F作用下小球a 从图示虚线位置开始缓慢向右移动. 已知两球的重力满足G_b=2G_a=2G，滑动摩擦力等于最大静摩擦力，小球a与细杆间的动摩擦因数为 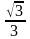. 则下列说法正确的是

A．当细绳与细杆的夹角为60°时，拉力F的大小为(2-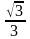 )mg

B．支架对轻滑轮的作用力大小逐渐增大

C．拉力F的大小一直增大

D．拉力F的大小先减小后增大

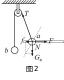解析 如图2，对a球进行受力分析可知，在缓慢移动的过程中a球受到重力G，水平拉力F，细绳的拉力T，可能受到杆对球的弹力N和摩擦力f. 其中，G_a保持不变，T大小不变（与b球重力在相等为2G）与水平方向夹角不断减小，N、f的大小和方向均待定. 显然用常规的正交分解来分析较繁琐，物体可能受到5个力的作用，直接用矢量三角形也不合适，因此考虑采用“多边形法则”来分析.

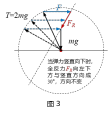
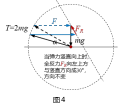
用F_R表示N与f的合力（称为全反力），因为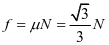 ，当N竖直向下时，F_R与竖直方向成30°向左下方（如图3）；当N竖直向上时，F_R与竖直方向成30°向左上方（如图4）. 利用“多边形法则”：物体在多个共点力作用下处于平衡状态时，平移各力矢量可构成首尾相连的闭合多边形. 观察图3不难发现，当细绳与细杆的夹角为60°时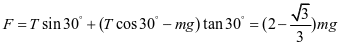， ，A项正确；细绳与细杆的夹角逐渐减小到30°的过程中，水平拉力F逐渐增大，支架对轻滑轮的作用力（即N与f的合力）逐渐减小到0，B项错误. 继续减小细绳与细杆的夹角，N方向反向，F_R与竖直方向成30°向左上方（如图4），从图中可知F随夹角增大而增大，综合可知，C项正确，B项错误.

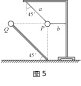例2 如图5所示，绝缘轻质细绳将带正电的轻质小球P悬挂在空中，a绳与竖直方向夹角为45°，b绳水平. 带负电的小球Q套在固定的绝缘细杆上，绝缘杆与水平地面间的夹角也为45°，杆的顶端与小球P等高，绝缘杆的底端在小球P的正下方. 则把小球Q从杆的顶端缓慢移动到底端的过程中，下列说法正确的是

A．a绳中张力先增大后减小

B．b绳中张力先增大后减小

C．小球Q位于绝缘杆的中点时，a、b绳中张力大小相等

D．小球Q位于绝缘杆的顶端和底端时，b绳中张力相同

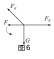
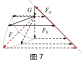
解析 对球P受力分析（如图6），球受到4个力的作用，其中重力G保持不变，绳上的拉力F_a和F_b方向保持不变，Q对P的库仑力F方向逆时针方向变化大小先变大后变小. 若用正交分解法讨论动态平衡过程中a、b绳中张力大小的变化情况较繁琐，考虑用多边形法则进行图解分析. 平移各力矢量构成首尾相连的多边形（如图7），因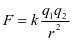 ，当两球连线与竖直方向成45°时F最大，其余位置其大小具有对称分布的特征（通过辅助圆可观察其大小变化）. 由图7易判断，当Q从杆的顶端缓慢移动到底端的过程中，F_a、F_b都先增大后减小，AB项均正确；当Q位于杆的中点时，库仑力F是初始位置时的2倍，但小球重力大小未知，无法判断F_a、F_b是否相等，C项错误；Q位于绝缘杆的顶端和底端时，b绳中张力相等，D项正确.

二、方法提炼

多个共点力作用下的动态平衡问题是较复杂的问题，分析此类时图解法的效率高于解析法. 一般而言，对于三力作用下的动态平衡问题可根据其受力特点选择“矢量三角形法”或“相似三角形法”. 但是对于受到四个以上作用力的动态平衡问题，则需要考虑将“三角形”法则拓展为“多边形法则”. 前文讨论的动态平衡物体受四个以上力的作用，受力分析后发现其中有一个力恒力，有两个力的方向不变，处理问题的步骤一般为：

1. “降维”：考虑是否可以通过逐步合成的方式，减少受力的个数. 如例1中，用全反力代替弹力与滑动摩擦力的，则五力平衡转变为四力平衡；

2. “定位”：找出多个作用力中大小和方向不变的那个力，确定这个力矢量为多边形的固定边，如例1、例2中的重力. 同时，找出一个方向不变但大小可能变化的力，过前面固定力矢量的末端确定一直线代表该力的方向；

3. “平移”：将其余几个力，根据其方向及大小变化的范围（例1中绳拉力大小不变方向改变，可用辅助圆个表示变化范围），平移各矢量线段使其构首尾相连的闭合多边形.

4. “旋转”：在变化范围内转动方向（至少画出三个不同位置）变化的那个力矢量，观察在力多边形中各边长的变化情况，得出结论.

正确地抓住多力作用下动态平衡的变与不变，灵活地应用“多边形法则”进行受力分析动态平衡问题，是对平行四边定则的深度理解和应用. 教学中，教师要适当引导学生对这一核心物理规律进行拓展，提高学生应用定性或半定量的方法解决问题的能力.

参考文献

[1]蒋天林. 对2017年理综卷_第21题题型的补充与拓展[J]. 中学物理教学参考, 2017, 46(12): 61-62.

[2]温卫国. 小议物体动态平衡问题[J]. 物理教学探讨, 2015, 33(8): 41-44.

本文为2019年福建省基础教育课程教学研究课题“基于高中物理学业质量水平的教学与评价研究”（立项批准号MJYKT2019-001）阶段性成果。

通讯地址：福建省福州市仓山区对湖路15号福建师大附中，350007

联系方式：李明哲，13605949420，lmz1978@126.com