重要极限与利息计算

重要极限与利息计算

翟维红

天津海运职业学院

摘要：在高等数学两个重要极限教学中，通过运用实例教学，激发学生的学习兴趣，使其增强探求新知的方法，即达到使学生对重要极限的深入理解与掌握，又养成良好的学习方法的目的。

关键词：重要极限 连续复利 应用

1. 引言

极限概念在经济生活中运用非常广泛，极限方法体现着无限逼近的思想。对于经济问题来说，无限逼近是相对的，实际问题中对于经济量的估算并不需要绝对精准，只要逼近次数足够多，误差小到合理范围内即可以逼近次数无限大来处理。连续复利公式就是通过这种方法求出的，并在实际工作中有着广泛的应用。

二、第二个重要极限

公式结构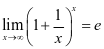： ，函数极限为 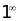型未定式极限，在这里给出一个直观说明，表明 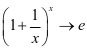， （如表1）。

表1（以数列极限为例）

显然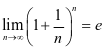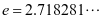， （ 是一个无理数），若 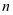取负整数值，列表同样成立。可以证明，此数列换成函数后极限仍成立，即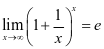

三、连续复利公式

（一）以年为期的复利公式

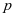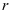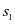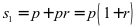设本金为 ，年利率为_，一年后的本利和为 ，则 ；把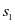 作为本金存入，第二年后的本利和为 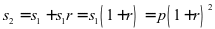；再把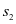 存入，如此反复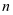， 年后的本利和为 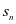，则以年为期的复利公式为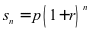： （1）。

（二）连续复利公式

若把一年分为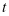 期计息，这时每期利率可认为是 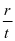，于是推得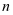 年的本利和为

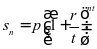，假设计息期无限缩短，则期权 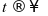，得到计算连续复利的公式为：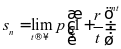

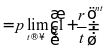
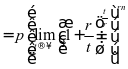
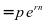
即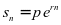， （2）

四、应用

例1、有本金10000元，存款一年，年利率1.75%，求到期本利之和。（1）按一年一期计息；（2）按连续复利计息。

解：（1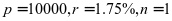） ，由公式（1）可得出到期本利和为：

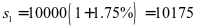（元）

（2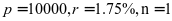） ，由公式（2）可得出到期本利和为：

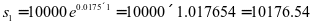（元）

经比较得出，利率非常低时，两种存款方式的收益区别不大。特别是在连续复利计息方式下随着计息期数的增加，利息虽然会有增加，但是随着期数不断增加趋于无穷时，本利和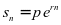 会趋于一个定数。故采取连续复利方式存款时本利之和并不会越来越多。目前银行存款利率都不是很高，存款人要想取得相对较高的回报可通过以下两种方式；一种是存期长，利率较高，不会要求起存门槛；另一种是存期短，但要求起存门槛，利率也较高。

例2、某单位2017年1月10日购置一台设备，贷款100万元，年利率5.25%，2021年1月10日到期，一次还本付息，求贷款到期时还款总额。（1）按一年一期计息；（2）按连续复利计息。

解：（1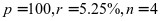） ，由公式（1）可得出到期还款总额为：

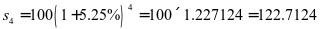（万元）

（2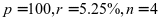） ，由公式（2）可得出到期还款总额为：

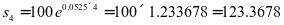（万元）

经比较得出，利率比较高时，两种还款方式的差异还是较大的。所以民间借贷时，某些贷款方为了取得高额的回报，往往采取连续复利的计息方式收取借款方的利息，一旦违约，后果不堪设想。所以有贷款需求时一定要通过正规渠道申请，避免发生借贷纠纷。

第二个重要极限结合实例讲解，能够提升学生学习数学的兴趣，并使学生感受到在数学课堂中不仅可以学数学，还能用数学的乐趣。

参考文献：

[1]李建平 曹定华．微积分(第五版) [M]．复旦大学出版社，2015（11）

[2]窦连江．高等数学(经管类专业适用) [M]．高等教育出版社，2006（9）

[3]梁素梅．第二个重要极限在复利问题中的应用[J]．数学学习与研究，2017（6）

作者简介：翟维红（1968—），女，天津市人，天津海运职业学院副教授，主要研究基础数学。通讯地址：天津海运职业学院社科部（300350），邮箱zhaiweih@163.com,联系电话13820907850。

1