基于数学核心素养下的“三角函数”教学设计研究

基于数学核心素养下的“三角函数”教学设计研究

王贤

广州大学附属东江中学 517500

摘要：高中数学核心素养的培养，是革新传统教育观念的一项重要举措，能够适应高中阶段学生的身心发展需要，也是践行素质教育理念的行为，因此，教师要从不同的核心素养角度入手，不断丰富课堂内容，着力提升课堂质量。文章主要阐述高中数学“三角函数”相关内容的教学设计，从核心素养的培养角度入手，研究合理的教学策略，为教师提供不同的教学思路。

关键词：高中数学；核心素养；三角函数；教学设计

引言：高中数学核心素养囊括数学抽象、逻辑推理、数学建模、数学运算等内容，培养学科核心素养从教学整体结构和课堂教学实施策略出发，旨在提升学生的综合素质能力。教师应当起到关键的引领和培育作用，遵照新课程标准要求和素质教育理念，营造良好的学习气氛，构建高效数学课堂。

一、深化基础培养数学抽象素养

数学抽象素养能够增强学生透过现象看本质的能力，使之能够迅速从不同内容中抽象出规律和结构，更好的理解知识，逐渐养成一般性思考问题的习惯，进而用抽象思维来审视问题，获得更多的解决思路。教师要注重基础知识讲解，深化学生的数学基础知识理解，培养其优秀的数学抽象素养。比如，在“任意角和弧度制”部分内容讲解的过程中，引导回忆角的相关知识，从运动的观点出发来引申出正角、负角、零角的知识，结合实际生活中的体现来进行讲解，激发学生的抽象思维，使之能够加深对任意角的理解。建立直角坐标系，并阐述“不存在于任何象限的角”相关问题，细致讲解象限角与非象限角的知识，深化学生的基础知识理解。再利用Flash动画呈现角始边与终边的运动轨迹，阐述度量角的单位制——角度制和弧度制，并引导其利用抽象思维来理解弧度，明白正角弧度数为正，负角弧度数为负，零角弧度数为零。通过深化基础知识讲解，切实提升了学生抽象思维能力，为后续的教学奠定了稳固基础^[1]。

二、启迪思维培养数学建模素养

建模素养是利用模型来解决问题的能力，可以让学生从不同的角度来审视问题，进而建立起知识与客观世界的联系，不断积累学习经验，针对不同的问题来建立模型，最终通过论证和改进，解决实际问题。教师在实际授课过程中，要利用各种工具来引导学生掌握建模的技巧，培养其优秀的建模素养。比如，在“三角函数的图象与性质”部分内容讲解的过程中，复习三角函数定义的相关内容后，研究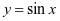 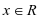， 的图像，引导学生利用模型思维来理解图像性质，加深对正弦曲线的理解。再借助正弦曲线来绘制余弦函数图像，根据诱导公式 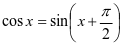来推导余弦函数 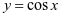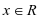， 的图像解析式，加深对余弦曲线的理解，再利用建模软件来呈现 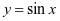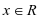， 的图像和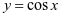 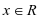， 的图像，研究相关性质。带领学生利用建模软件来分析图像的周期性，理解周期、周期函数、最小正周期的内容，再通过观察图像中的曲线变化来研究奇偶性，明白正弦函数为奇函数，余弦函数为偶函数。随机选择一个周期区间，讨论函数的单调性，使学生能够通过建模来理解两函数的增减变动，从而根据单调性来判断最值问题，形成优秀的建模素养^[2]。

三、注重解析培养逻辑推理素养

逻辑推理素养能够提升学生的推理能力，有助于把握知识之中的严谨性，利用良好的思维品质进行交流，从而掌握基本的推理形式和规则，深化对不同结论的理解，构建起清晰的知识体系。教师需要注重不同知识的解析，为学生构建清晰的知识脉络，培养其优秀的逻辑推理素养。比如，在“三角恒等变换”部分内容讲解的过程中，从不同的诱导公式出发，引导学生对三角函数式进行恒等变形，推理相关的恒等关系，使之能够在探究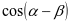 和角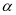 、 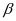的正弦余弦之间的关系，推理得到差角余弦公式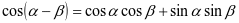： 。再根据以上公式推理两角和余弦公式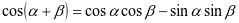： ，教师带领其进一步推导，得出两角和与差正弦公式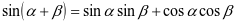： 和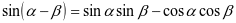 。鼓励其基于上述公式来推导两角和与差正切公式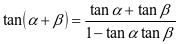： 和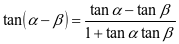 。再进行细致的解析和总结，为学生构建清晰的知识脉络，使之能够在反思推理的过程中理解和角公式和差角公式，再推导倍角公式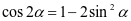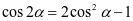： ， ，明确探究三角函数之间关系的方法，进一步加深对恒等变换的理解。

四、注重实践培养数学运算素养

数学运算素养是提升实践技能水平和应试能力的必备素养，学生可以利用有效的方法来解决实际问题，促进思维发展，养成良好的解题习惯，树立起科学的精神态度。因此，教师要从实践的方向入手，结合实际问题来培养学生的数学运算素养，使之能够秉持严谨求实的精神来进行运算，进而提升实践技能水平和应试能力。比如，在“三角函数的应用”部分内容讲解的过程中，可以出示生活中交通警察处理超速的案例，激发学生的求知欲和探究兴趣，带领其从三角函数角度来分析案例中涉及的知识，并引申出授课内容。利用测量古塔高度的实际问题，归纳用三角函数解题的步骤，再利用台风案例来归纳一般解题思路，出示弹簧振子实验的视频，引导学生记录相关实验数据，利用函数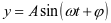 来计算振子振动位移随时间的变化规律，进而制作散点图，算出相关的解析式，加深对振幅、周期、频率、相位、初相等概念的理解，在分析具体的超速、古塔测量、台风等案例中提升运算能力，形成优秀的核心素养。

结束语：

总而言之，高中数学教师需要从不同的核心素养内涵入手，把握教学和学习兴趣之间的联系，激发学生数学学习的兴趣，使之能够发挥主观能动性学习数学知识，为教师的相关工作开展提供良好的保障。也要注重启发和思维培养，精准把握数学理论内容的本质，从而优化教学，切实提高课堂教学质量，助力学生成为高素质人才。

参考文献：

[1]包悦玲,赵思林,汪洋.高中数学单元教学研究综述[J].内江师范学院学报,2020,3510:18-22.

[2]王雅琴.刍议高中数学核心素养的教育价值及教学渗透策略[J].张家口职业技术学院学报,2018,3101:79-80.

[3]刘世科.高中数学教学策略探讨——以“三角函数”教学为例[J].西部素质教育,2019,509:238.

本文系广东省河源市课题《在新课标视域下基于东源学情的高中数学教学设计研究一一以三角函数为例》（课题编号：DYGH2019GZ05）课题阶段性研究成果.