飞艇高可信度CFD技术研究

飞艇高可信度CFD技术研究

王昆仑

（中国特种飞行器研究所，荆门，448035）

摘要在飞行器的CFD计算中，计算网格的类型、网格数量、网格质量以及求解时湍流模型的选取，对计算效率和计算结果的准确度有着决定性的影响。本文分别从计算网格类型、网格数量以及湍流模型三方面入手，通过CFD计算与试验值对比分析，得出了适用于飞艇气动特性计算的CFD方法。研究结果表明，采用笛卡尔网格、1/120网格单元尺寸比、SST k-w湍流模型可以得到高可信度的飞艇CFD计算结果。

关键字：CFD、计算网格、湍流模型

1概述

飞艇等低速飞行器的性能受风场和其它外界因素影响很大，在设计阶段，需要得到其全面的气动特性，为后续设计提供指导。随着计算流体力学和计算机技术的高速发展，应用CFD软件对飞艇的气动特性进行计算，并通过后期的风洞试验假以验证，从而得到可靠的气动数据是现在飞艇设计研究的一般方法。在进行CFD仿真计算时，针对具体的几何外形，计算网格类型的选用、计算域网格数量的确定以及计算湍流模型的选取对最终计算结果的准确性和计算效率具有极大的影响，因此，针对这几方面开展研究是很有必要的。

1.1网格类型简介

目前主流的计算网格类型包括结构网格、非结构网格和笛卡尔网格（图1）。

结构网格可以很容易地实现区域的边界拟合，网格生成速度快、网格质量好、数据结构简单；但结构网格的适用范围窄，针对复杂外形网格划分过程复杂、对操作人员经验要求高，难度大，耗时长。

非结构网格多件三角形网格和四面体网格，采用随机的数据结构有利于网格自适应；网格划分相对简单，但单元网格的正交性较结构网格差，计算精度和收敛速度均低于结构网格。

笛卡尔网格为六面体贴体网格，网格生成过程中不需预先生成严格规定的某种物面网格，生成过程统一，不需要人为干预，相比于结构网格和非结构网格，是真正的自动化网格，但其网格生成算法导致切割过程中可能形成微小的网格单元，造成方程系统的刚性问题。

图1三种网格类型

1.2网格数量对CFD计算的影响

计算域内的网格数量，直接决定了求解的代数方程组的数量，并直接影响仿真计算的准确度和求解计算的耗时。计算域网格数量主要由几何模型面网格数量、附面层网格数量以及部分加密区网格数量决定。面网格数量在本文中通过网格单元尺寸比（面网格单元尺寸与几何模型特征长度之比）来反映；附面层网格数量可由y+（附面层第一层网格高度的无量纲表征值）确定；加密区的位置和网格数量需根据具体的几何外形特征来确定。网格数量在达到一定规模后，继续增加网格数量并不能提高计算的准确度，反而延长了求解计算的时间，降低计算效率，因此，确定满足计算要求的网格数量，是本文工作的重点之一。

1.3湍流模型简介

工程应用中主流的湍流模型包括Spalart-Allmaras模型k-ε型、k-ω模型、v2-f模型、转捩k-kl-ω模型、转捩k-ω模型、雷诺应力RSM模型、分离涡模型等。虽然目前已经提出了多种湍流模型，但是还没有适用于各种流动现象的湍流模型。湍流模型的选择取决于流动包含的物理问题、精确性要求、计算资源的限制、模拟求解时间限制。

常用的适合浮空器气动计算的湍流模型有Spalart-Allmaras（SA）和SST k-ω模型。

SA模型是只求解一个修正粘性输运方程的计算量较少的RANS模型。在修正形式下，近壁区的涡粘性更容易被求解。它包含了一组新的方程，在这些方程里不必去计算和剪切应力层厚度相关的长度。SA模型主要在空气动力学和流体机械等含有中度分离现象的场合被使用。

标准k-ω模型时基于Wilcox k-w模型，为考虑低雷诺数、可压缩流动和剪切流动传播而修改的。Wilcosk-ω模型能预测自由剪切流传播速率，如尾流、混合流动、平板绕流、圆柱绕流和放射状喷流，因此可以将其应用于墙壁束缚流动和自由剪切流动。而SST k-ω与标准k-w模型相似，但SST k-ω模型比标准k-w模型在广泛的流动领域中有更高的精度和可信度。

2几何模型

本文计算采用的模型为某试验艇的缩比模型（图2），缩比比例为1/45，模型长度1.2388m，体积0.066m3。

图2几何模型

3网格划分

分别对几何模型进行结构网格、非结构网格和笛卡尔网格的划分，通过网格单元尺寸比和附面层y+值控制网格数量。本文选取1/120、1/240、1/480三种比例，y+=1、y+=60两种附面层控制策略，共生成18套计算网格，其中结构网格的网格数量为390万到1358万，非结构网格的网格数量为475万到1420万，笛卡尔网格的网格数量为586万到942万，部分网格图见图3。

图3三种网格尺寸

4计算方法

采用商业软件进行数值计算，压力速度耦合采用SIMPLE算法，压力、密度等耗散项采用二阶迎风格式；入口边界为速度入口，出口边界为压力出口。

5计算工况

计算模型采用近地面大气参数进行计算，以保证与风洞试验参数的一致，方便计算结果与试验结果的对比分析。

计算攻角范围为0°—20°。

6计算结果分析

6.1 不同网格类型计算结果对比

采用1/120网格单元尺寸比的结构网格、非结构网格和笛卡尔网格的网格数量分别为390万、1000万和586万，选择SST k-ω湍流模型，通过计算得到图4的飞艇纵向气动数据与实验数据对比结果。可以直观看出，结构网格和笛卡尔网格的计算结果相较试验值，偏差较小，其中，升力和阻力特性与试验值重合度很高；非结构网格的计算结果则与试验结果偏差较大。

图4不同网格纵向气动特性对比

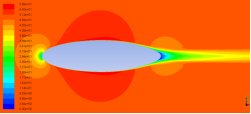
另外，由图5各网格类型剖面速度云图可以看出，结构网格和笛卡尔网格流场速度分布符合一般规律，尾流段模拟效果良好；非结构网格对尾流捕捉能力较差。

综合考虑，非结构网格在相同网格单元尺寸比时网格数量最多，计算结果较试验值偏差大，流场模拟不如其他两种网格精确，因此，非结构网格不适合飞艇的CFD计算。

图5不同网格剖面速度云图

6.2 不同网格尺寸对比

前一小节计算得出非结构网格不适合飞艇CFD计算的结论，本小节分别对不同网格单元尺寸比的结构网格和笛卡尔网格的气动特性进行对比分析，以确定满足飞艇CFD计算要求并且计算效率较高的网格数量。

由图6可以看出，对于结构网格，三种不同网格单元尺寸比的网格的计算结果都非常接近，且均与试验值贴合度较高，满足计算要求。而1/120网格单元尺寸的网格数量为390万，远小于其他两个尺度的网格数量，计算耗时少，效率高，因此，在结构网格划分时，采用1/120网格单元尺寸比最适合飞艇的CFD计算。

图6结构网格不同单元尺寸比纵向气动特性对比

由图7可以看出，对于笛卡尔网格，与结构网格的计算结果类似，三种不同网格单元尺寸比的笛卡尔网格的计算结果也非常接近，且均与试验值贴合度较高，满足计算要求。1/120网格单元尺寸比的网格数量为586万，小于其他两个尺度的笛卡尔网格数量，高于相同网格单元尺寸比的结构网格的数量。因此，在笛卡尔网格划分时，采用1/120网格单元尺寸比可以满足飞艇的CFD计算要求。

图7笛卡尔网格不同单元尺寸比纵向气动特性对比

6.3 不同湍流模型对比

分别采用有Spalart-Allmaras（SA）和SST k-ω模型进行飞艇的CFD计算，由图8和图9可以看出，无论结构网格还是笛卡尔网格，在小迎角时，SA和SST k-ω模型的计算结果非常接近，而在迎角较大时，SST k-ω模型的计算结果相比于SA模型更靠近试验值。因此，SST k-ω模型更符合计算要求。

图8结构网格不同湍流模型纵向气动特性计算结果

图9笛卡尔网格不同湍流模型纵向气动特性计算结果

综上，对飞艇进行CFD仿真计算时，采用结构网格或笛卡尔网格，网格单元尺寸比为1/120，计算湍流模型为SST k-ω，可以保证数值计算的准确性，同时具有较高的计算效率。

7结论

非结构网格在相同网格单元尺寸比时网格数量最多，计算结果较试验值偏差大，流场模拟不如其他两种网格精确，因此，非结构网格对于浮空器的CFD计算要差于结构网格和笛卡尔网格。

采用1/120网格单元尺寸比划分结构网格和笛卡尔网格，得到的计算结果均满足计算要求。虽然相同尺寸比的笛卡尔网格数量多于结构网格，但考虑到处理复杂外形时（如包含舵面缝隙的模型），结构网格的生成难度远高于笛卡尔网格，因此，笛卡尔网格更适合飞艇的CFD计算。

无论结构网格和笛卡尔网格，在小迎角时，SA和SST k-ω模型的计算结果非常接近，而在迎角较大时，SST k-ω模型的计算结果相比于SA模型更靠近试验值，因此，SST k-ω模型更符合计算要求。

参考文献

[1] 王福军编著：《计算流体动力学分析》，清华大学出版社，2004年9月。

[2] 李栋、杨永等译著《空气动力学基础》，航空工业出版社，2010年2月。

[3] 王瑞金、张凯、王刚编：《Fluent技术基础与应用实例》，清华大学出版社，2007年2月。

[4] 郭然、贾力平等编：《NUMECA系列教程》，机械工业出版社，2013年3月。