深度探究提素养  逐层深入现本质------从课本的一个“探究活动”说起

深度探究提素养  逐层深入现本质------从课本的一个“探究活动”说起

章建飞

兰溪市第八中学

摘要：如何将“一个已知三个内角的三角形分割成两个等腰三角形”？可以通过不断试错的方法解决问题，那么“任意一个三角形可以分割成两个等腰三角形”吗？如何将“任意的一个三角形分割成两个等腰三角形”呢？这些问题需要通过精心设计探究路径才能解决，即做到有效探究。从给出具体角度的三角形抽象到任意的三角形，逐层递进，最终探得问题本质。探究是思考和解决数学问题的重要方式，是培养和提升核心素养的有效途径。本文通过八（上）浙教版教材里的一个探究活动展开思考。

关键词：等腰三角形；深度探究；分类讨论

探究活动即探究性学习，探究性学习，即Hands-on Inquiry Based Learning（HIBL），指学生在学科领域内或现实生活情境中选取某个问题作为突破点，通过质疑、发现问题；调查研究、分析研讨，解决问题；表达与交流等探究学习活动，获得知识，掌握方法。在新课标下，探究活动在培养核心素养方面更能体现其优越型。

1   问题呈现

在八（上）浙教版的数学教材里有这样一个探究活动：

如图，有丙、丁两个三角形.丙三角形的内角分别为10°，20°，150°；丁三角形的内角分别为80°，25°，75°.你能把每一个三角形分成两个等腰三角形吗？画一画，并标出各角的度数.

               丙                            丁

这个题目的解并不难找，学生通过“凑一凑”就能实现，再不行通过小组合作也很快能找到答案。

图丙中，只要考虑三种情况。一是：将20°分出10°验证；二是将150°分出10°验证；三是将150°分出20°验证。

图丁中，也是考虑三种情况。一是：将75°分出25°验证；二是将80°分出25°验证；三是将80°分出75°验证。答案如下：

             丙                              丁

这个题如果就这样简简单单的分析一下，找个答案就结束那就太可惜。课本在《等腰三角形的判定》这节课设计此探究活动的目的有两个：

一是巩固本节课所学内容，即等腰三角形的判定方法，通过角的角度来判断；

二是通过这个探究活动的实施，让学生积累活动经验，让学生去探寻分法背后的一些基本思考方法，促进探究能力的提高，形成有效探究；

三是在探究的过程中，既能提升学生的“四基四能”，更能提升学生的抽象能力、推理能力、模型观念等核心素养。

2   理论思考

初中数学探究活动是学生通过实际操作、观察、发现、思考、探索等路径，去发现某些数学问题的结论或规律，是一种主动探讨和研究。为学生提供一个平等交流的机会，让学生自由表达观点、相互质疑、激烈讨论、思想碰撞，它把目标指向培养学生的核心素养，如归纳能力、创新能力、问题意识、合作能力等，而不仅仅是停留在知识的掌握或继承。

所以组织探究活动的意义有四重境界。一是通过探究活动，可以充分培养学生的团队合作意识，在质疑、讨论中思维碰撞，形成基本活动经验；二是通过探究活动，可以发现解决一些典型数学问题的通性通法或本质规律，以掌握更多的数学知识；三是通过探究活动，能让学生掌握研究数学问题的一些基本思考方法、策略；四是将探究活动所得的思考方法、内在规律进行重组、创新，最后服务于生活，为人类发展作贡献。

3   问题重设

基于这样的培养理念，本节课的探究活动就是一个很好的契机。我们可以以问题启发为导向，将问题探究分层设计，逐步深入，直至问题的核心，收获一些显性成果和解决方法。

在解决完原题后，引导学生思考：（1）在图丙中，经过其中任一顶点的分割线，分出一个等腰三角形有多少种分法？（2）任意的一个三角形都能分割成两个等腰三角形吗？（3）具备什么样条件的三角形一定可以分割成两个等腰三角形？显然，这三个问题比原题有意思多了，思维量明显增加，学生的学习积极性和主动性很快的就调动起来了。

接下来，对这三个问题逐一探究即可。

探究问题（1）：如图，过△ABC的任一顶点作一条直线分割线，分割出一个等腰三角形，有多少种分法？.

设计意图：从一个已知三个内角的三角形中分出一个等腰三角形，问题相对简单，找出一种、二种分法都比较容易，但要找出所有分法却有难度，为什么呢？显然是学生没有掌握基本的思考方法。

错误思考1：分别以三角形的三个顶点为圆心、任一边长为半径画弧线，如图：

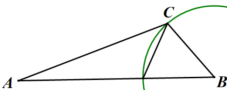
            AC为腰                                  BC为腰

             BC为腰                                  BC为腰

思维漏洞是：从边的角度思考，但只考虑了三边长为腰的情况，没有考虑三边为底的情况，造成漏解.

错误思考2：分别以20°和50°为相等角构成的等腰三角形.

思维漏洞是：从等角的角度思考，但只考虑了分别以20°和50°为底角的情况，没有考虑为顶角的情况，造成漏解.

综合看，就是没有掌握好这个问题分类讨论的基本思路。

那么这个问题该如何分类呢？其实只要把学生的讨论加以总结即可.

若以“边”分类，则三边分别可以为腰，也可以为底。正确结果如下：

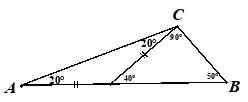
           AC为腰                                  AC为底

AB为底，AB为腰不存在                        BC为腰

            BC为腰                                BC为腰

 BC为底

若以“角”分类，则三个角分别可以为顶角，也可以是底角。正确结果如下：

           ∠A为顶角                     ∠A为底角（顶点在AB上）

∠A为底角（顶点在AC上）               ∠B为顶角

       ∠B为底角（顶点为点C）             ∠B为底角（顶点在AB上）

∠C为顶角（∠C为钝角，故∠C为底角时不存在）

综上可知：不管以“边”分类，还是以“角”分类，都存在两种情况：即边可以是腰，也可以是底；角可以是顶角，也可以是底角。只有抓住边角的分类，形成基本知识框架和基本思考方法，就能做到不漏解的完整解答。

探究问题（2）：已知任意△ABC，若要分割成两个三角形，一定能分成两个等腰三角形吗？

对于这个问题可以逆向思考，即只要举出一个反例即可。

如图，△ABC为等边三角形，每个内角都为60°。显然，将这个等边三角形分割成两个三角形，不管你如何分，都无法分出等腰三角形，更别说两个。

顺势提出探究问题（3）。

探究问题（3）：已知任意△ABC，需满足什么条件，必定能分割成两个等腰三角形？

设计意图：书本原题中，给定的两个三角形都是确定了角度，可以通过不断试错法达到目标，但思维量是明显不够的，所以探究一个更有思维深度的问题就显得十分必要。

已知△ABC，如何将△ABC分割成两个等腰三角形？这个问题背后其实有三个问题：

问题①：由探究问题（2）可知，既然不是任意一个△ABC都可以分割成两个等腰三角形，那么满足什么条件之后就可以呢？

问题②：我们通过什么方法去探究问题①的答案，从什么角度去探究？

本探究活动中第一个要解决的问题是：从哪里画分割线？学生通过简单的思考便可得出，只能从任意一顶点处画分割线，只有这样才能分割成两个三角形。然后再思考：如何才能分成两个等腰三角形。

从上课的过程中可以看出，学生的第一思维是，凑的办法，从本质上讲这是最好的最直接的办法。几何直观就是一个好方法。学生会不断地去试探，直到达到目标。但是，这个思路应是已知了三个角的度数的前提下，现在是任意的一个三角形，那么如何思考呢？

在探究一个数学问题时，人们往往喜欢从具体的数值入手。当探究无法进行时，需要找到一个新的切入口。从任意三角形的“任意”两个字入手，我们可以从三角形的分类切入，先从特殊的直角三角形入手，体现从特殊到一般的数学思想。

①以三角形的不同类型为切入口进行探究。

如图1，在Rt△ABC中，点C为直角顶点，画出斜边上的中线CD，即可将△ABC分成两个等腰三角形，与∠A、∠B的度数大小无关。所以可以得出，任意Rt△ACB，只要画出“斜边上的中线”这条分割线即可分出两个等腰三角形。显然，直角三角形一定可以分割成两个等腰三角形。

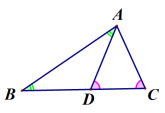
          图1                     图2                       图3

那么，锐角三角形如何分割成功呢？可以逆向思考：                                         

如图2，若锐角△ABC刚好被分成两个等腰三角形△DAB和△ACD，其中∠C=∠ADC，∠DAB=∠B。不妨设∠DAB=∠B=α，则∠ADC=∠C=2α，即∠C=2∠B，也就是说在锐角△ABC中，只要满足∠C=2∠B，就可以按图2 的方法将其分为两个等腰三角形。当然，还需要注意的地方是，既然是锐角三角形，那么要满足，

即，解得30°＜α＜45°.    

如图3，若锐角△ABC被分成两个等腰三角形△DAB和△CAD，其中∠DAC=∠ADC，∠DAB=∠B。不妨设∠DAB=∠B=α，则∠ADC=∠DAC=2α，即∠BAC=3∠B，也就是说在锐角△ABC中，只要满足∠BAC=3∠B，就可以按图3 的方法将其分为两个等腰三角形。当然，同样需要注意的是，既然是锐角三角形，那么要满足，

即，解得22.5°＜α＜30°.

如图4，若锐角△ABC已被分成两个等腰三角形△ABD和△DAC，其中∠DAC=∠C，∠DAB=∠B。不妨设∠DAB=∠B=α，则∠DAC=∠C=

=90°-α，即∠BAC=90°-α+α=90°，即△ABC是直角三角形，与△ABC是锐角三角形矛盾，此种情况下不存在.

由以上分析发现，在锐角三角形中，若最小的锐角在22.5°＜α＜30°范围时，且还有一个内角是这个最小角的3倍，则此锐角三角形一定可以分割成两个等腰三角形；若最小的锐角在30°＜α＜45°范围时，且还有一个内角是这个最小角的2倍，则此三角形一定可分割成两个等腰三角形；若最小的锐角α=30°时，且还有一个内角是这个最小角的2倍或3倍，则此三角形为直角三角形，一定可以分割成两个等腰三角形；

       图4                     图5                     图6

同样的道理，任意的一个钝角三角形也可以这样去探究。                                                       

如图5，若钝角△ABC刚好被分成两个等腰三角形△DAB和△ACD，其中∠C=∠ADC，∠DAB=∠B。不妨设∠BAC是钝角，设∠DAB=∠B=α，则∠ADC=∠C=2α，即∠C=2∠B，也就是说在钝角△ABC中，只要满足∠C=2∠B，就可以按图5 的方法将其分为两个等腰三角形。当然，还需要注意的地方是，既然是钝角三角形，那么要满足，  即，解得0°＜α＜30°；                 

如图6，若钝角△ABC已被分成两个等腰三角形△DAB和△CAD，其中∠CAD=∠ADC，∠DAB=∠B。不妨设∠BAC是钝角，设∠DAB=∠B=α，则∠ADC=∠CAD=3α，即∠CAB=3∠B，也就是说在钝角△ABC中，只要满足∠CAB=3∠B，就可以按图6 的方法将其分为两个等腰三角形。当然，还需要注意的地方是，既然是钝角三角形，那么要满足，此时∠CAB是钝角，即，解得30°＜α＜45°；若∠C是钝角，则有，解得0°＜α＜22.5°.

由以上分析发现，在钝角三角形中：

若最小角α满足0°＜α＜22.5°范围，且还有一个内角是2α或3α度时，则此钝角三角形可分割成两个等腰三角形；

若最小角α满足22.5°＜α＜30°范围，且还有一个内角是2α度时，则此钝角三角形可以分割成两个等腰三角形；

若最小角α满足30°＜α＜45°范围，且还有一个内角是3α度时，则此钝角三角形可分割成两个等腰三角形；

若最小的锐角α=30°时，且还有一个内角是这个最小角的2倍或3倍，则此三角形为直角三角形，一定可以分割成两个等腰三角形。

基于以上探究结果，可用表格归纳如下：

综上可得：在锐角或钝角三角形中，设最小角为α，且0°＜α＜45°，同时存在另一内角是2α或3α度，则此三角形一定可分割成两个等腰三角形；直角三角形一定可以分。

②以已形成的两个等腰三角形为切入口进行探究。

         图7                     图8                      图9

假设：确定△ABC已被分成两个等腰三角形△ABD和△ACD，其中∠DAB=∠B。设∠B=α，则等腰三角形△ACD中分三种情况讨论即可。

如图7，若∠C=∠ADC，只要满足∠C=2∠B=2α，即可分，此时0°＜α＜45°；

如图8，若∠DAC=∠ADC，只要满足∠BAC=3∠B=3α，即可分，此时0°＜α＜45°；

如图9，若∠C=∠DAC，此时∠BAC=90°（0°＜α＜90°），可分.

综合分析可知，此结论与前面探究方法得到的结论是一致的。

4   思考提升

4.1  深度探究的意义

要探寻某一数学问题的本质，用深度探究的方式是一种重要手段。有些数学问题适合初步探究，只是做一些初步的尝试，一些较浅的思考，点到为止；有些问题本身有深度，适合深入研究，有深度探究的价值，这类问题需要探得问题的本质以体现数学的价值所在。深度探究有助于培养学生勇于质疑和善于反思的习惯，培养学生发现、提出、解决数学问题的能力；有助于发展学生的创新意识和实践能力。

4.2 深度探究的设计框架

4.3 深度探究的设计原则

如何设计合理有效的“深度探究”路径，需要深入思考、不断打磨。“深度探究”需要满足三个原则：一是有效性原则，二是科学性原则，三是可操作性原则。

怎样的探究才是有效的、有意义的，有深度的？只有直面最基本的问题，逐层拨开知识的本源，才能提升学生的思维能力，更重要的是培养了学生对问题的探究方法的探寻，学生会将方法进行迁移，会展开对其它未知问题的探究思考。

“深度探究”活动的设计需要做好以下三点：

（1）利用好课本资源，发挥学生的主动性，将各种资源充分整合，选好深度探究问题；

（2）精心设计好探究问题的层次性，逐步深入，以满足不同层次学生的素养发展；

（3）通过深度探究活动有效实施，形成“有究必挖、有法必纳”的基本活动经验。

参考文献：

[1]义务教育课程标准：2022年版/中华人民共和国教育部制定.北京：北京师范大学出版社，2022.4

[2]义务教育课程标准（2022年版）课例式解读.孙晓天，沈杰主编.北京:教育科学出版社.2022.6

[3]胡柳青.问题引领课堂 促进深度学习[J].中学数学教学参考(中旬），2022（5）35-37.

[4]沈尚.开放问题背景下的单元复习课例思考[J].中学数学教学参考(中旬），2022（5）:35-37.