初中数学中与平行四边形有关的常见题型及解题策略

初中数学中与平行四边形有关的常见题型及解题策略

仲伟

四川省广元市苍溪县思源实验学校  628400

摘要：平行四边形是初中数学中一个非常重要的概念，涉及到了证明.计算和应用等方面。掌握与平行四边形相关的常见题型和解题策略对于学生的数学能力提升具有重要意义。

关键词：初中数学；平行四边形；解题策略

引言

在初中数学中，平行四边形出题的频率较高，主要考查平行四边形、菱形、矩形、正方形的定义、性质和判定，以及利用性质和判定进行相关计算和证明，各种题型均有涉及．近几年，又出现了以特殊平行四边形为背景的开放题、应用题、阅读理解题、学科间综合题、动点问题、折叠问题等热点题型．对于不同类型的题目，我们需要灵活运用解题策略来解决问题。

一、平行四边形的基本概念

平行四边形是初中数学中一个重要的几何概念。下面将介绍平行四边形的基本概念和相关性质。对于一个四边形来说，如果它的对边是互相平行的，则该四边形被称为平行四边形。平行四边形的对边相等。平行四边形的两条对角线互相平分，即两条对角线的交点是对角线的中点。平行四边形的相邻内角互为补角，也就是说，相邻内角的和等于180度。平行四边形的对角相等。平行四边形中特殊的情况有矩形.菱形.正方形。如果平行四边形的一个内角为直角，则称为矩形；如果平行四边形的一组邻边相等，则称为菱形。除了上述的定义和性质外，平行四边形还有一些其他的特征和定理，涉及到其内角、外角和边长的关系等。通过对其性质和定理的学习和运用，可以帮助我们解决与平行四边形相关的各种数学问题，如证明.计算周长、面积，判断形状等。

二、常见题型及解题策略

（一）判断是否为平行四边形

在判断一个四边形是否为平行四边形的题目中，我们可以利用平行四边形的定义和判定来进行。如果一个四边形的对边分别平行或长度相等，那么这个四边形就是一个平行四边形。所以，当题目给出四边形的各边长度并且判断它们是否平行四边形时，我们可以通过比较对边的长度是否相等来判断。矩形和菱形也是特殊的平行四边形，它们有额外的属性可以辅助判断。例如，如果一个四边形的一个角是直角，并且对边分别相等，那么这个四边形就是一个矩形。而如果一个四边形的对边分别相等，且一组邻边分别相等，那么这个四边形就是一个菱形。所以，在判断是否为平行四边形时，体会和掌握类比的学习方法：类比平行四边形来学习矩形、菱形与正方形，注意平行四边形、矩形、菱形与正方形之间的关系．

（二）计算平行四边形的周长

平行四边形的周长可以通过已知条件来求解。如图，□ABCD的周长为60 cm，对角线AC、BD相交于点O，△AOB的周长比△DOA的周长长5 cm，求这个平行四边形各边的长．

引发学生思考平行四边形周长为60 cm，即相邻两边之和为30 cm.△AOB的周长比△DOA的周长长5 cm，而AO为公共边，OB＝OD，因而由题可知AB比AD长5 cm，进一步解答即可．平行四边形被两条对角线分成四个小三角形，相邻两个三角形的周长之差等于邻边边长之差．

另外，如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD，交BC于点E，若△CDE的周长为10，则平行四边形ABCD的周长是多少？

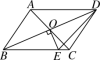
引发学生思考由平行四边形的性质得出AB＝CD，BC＝AD，OB＝OD，再根据线段垂直平分线的性质得出BE＝DE，由△CDE的周长得出BC＋CD＝10，即可求出平行四边形ABCD的周长．本题考查了平行四边形的性质、线段垂直平分线的性质以及三角形、平行四边形周长的计算；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．

（三）计算平行四边形的面积

平行四边形的面积计算公式是底边×高。在计算面积时，需要确保底边和高垂直。如果给出的是斜边和高的长度，我们可以利用勾股定理来求解底边的长度，然后再计算面积。如图，在□ABCD中，AB＝10，AD＝8，AC⊥BC.求BC、CD、AC、OA的长以及□ABCD的面积．

引发学生思考根据平行四边形边、对角线的长度求所求线段的长，根据S□ABCD＝BC·AC求解．

一位饱经沧桑的老人，经过一辈子的辛勤劳动，到晚年的时候，终于拥有了一块平行四边的土地，由于年迈体弱，他决定把这块土地分给他的四个孩子，他是这样分的：当四个孩子看到时，争论不休，都认为自己分的地少，同学们，你认为老人这样分合理吗?为什么?平行四边形的对角线将其分为四个面积相等的三角形。

另外还有如，欢欢看到平行四边形的草地一处有一水井，为了浇水的方便，欢欢建议我们经过水井修小路，一样可以把草地分成面积相等的两部分，同学们，你知道聪明的欢欢是怎么分的吗？

（四）综合运用平行四边形的性质

综合运用平行四边形的性质是一种要求学生结合已知条件并运用平行四边形的性质解决实际问题的题型。在解题过程中，我们需要仔细分析题目给出的条件，并利用平行四边形的性质进行推理和计算。一些常见的方法包括使用平行四边形的对边平行、对角线互相平分等性质。例如，如图，在四边形ABCD中，AC⊥BD， BD=12，AC=16，E、F分别为AB、 CD的中点，求EF的长．

在综合运用平行四边形的性质时，我们需要根据已知条件进行推理，并运用适当的性质和定理来解决问题。

（五）证明题型

在证明题型中，学生需要基于平行四边形的定义和性质推导出结论。解题时，我们要明确题目要求证明的命题，并确定证明的步骤。常见的证明方法包括使用平行四边形的定义、性质和基本定理，并运用逻辑推理和几何证明方法。通过证明题型，我们可以深入理解平行四边形的性质和特点，并培养逻辑思维和证明能力。如图所示，在四边形ABCD中，AD∥CB，且AD＞BC，BC＝6 cm，动点P、Q分别从A、C同时出发，P以1 cm/s的速度由A向D运动，Q以2 cm/s的速度由C向B运动，则2秒后，四边形ABQP为平行四边形．

结束语

综上所述，通过掌握与平行四边形相关的常见题型和解题策略，可以帮助学生提高解题能力，并且拓宽对数学知识的理解。在解题过程中，学生需要善于分析问题，熟练运用平行四边形的性质和公式，以及进行逻辑推理和几何证明。只有不断地练习和思考，才能够在数学学习中取得更好的成果。

参考文献

赵焱.初中生平行四边形CPFS结构分析研究[D].云南师范大学,2020.

.